Foro de dudas del práctico 2

Buenas.

Tu procedimiento y tus cuentas parecen estar bien.

De todas formas el sistema tiene infinitas soluciones. Esto es porque, si bien de las ecuaciones se deduce que debe ser 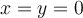$x=y=0$, estas no te imponen restricciones sobre la coordenada $z$.

Por lo tanto el subespacio propio (de la matriz asociada) es: 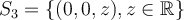$S_{3} = \{(0,0,z), z \in \mathbb{R} \}$. En este caso coincide con el subespacio propio de T, por estar usando la base canónica.

Como comentario general: los subespacios propios siempre tienen dimensión al menos 1. En particular esto quiere decir que: si llegaste a que el subespacio propio es el subespacio trivial, entonces hiciste algo mal.