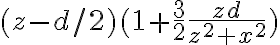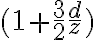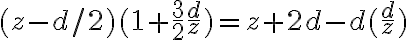Hasta ese punto comprendo la resolución sin problemas.
No entiendo en la solución colgada en el Eva, de dónde sale el entonces que iguala r2^-3 a otras cosas.
Buenas! La igualdad sale por el torema de Pitágoras en el triángulo de la figura, que tiene lados x y (z+d/2). El entonces no es porque se deduzca de lo que está inmediatamente antes
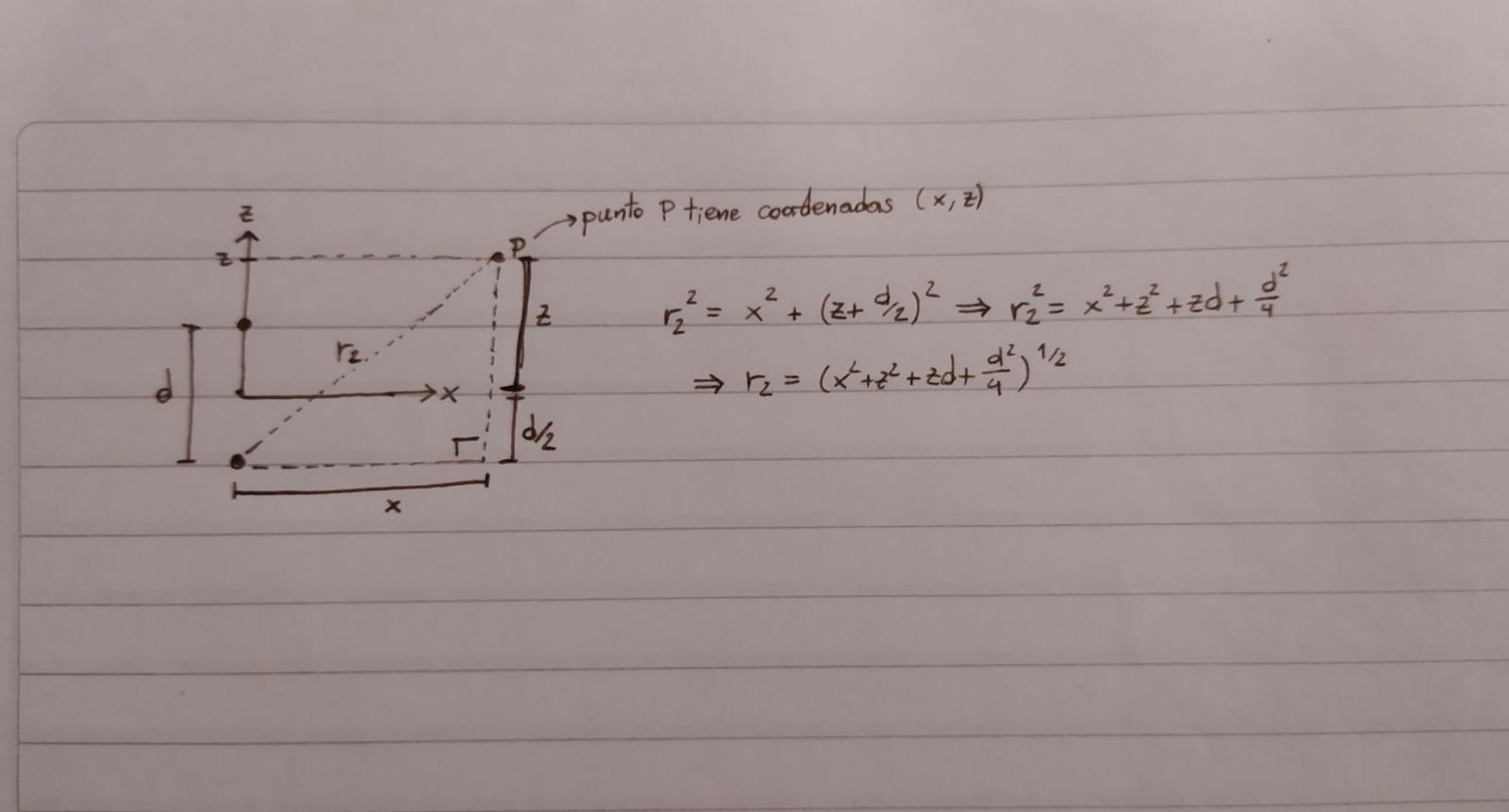
Muchísimas gracias! Ahora entendí lo más bien. Sin embargo, terminé el ejercicio y me quedó otra duda, ¿por qué podemos despreciar al final el término con d² en Ez?
Hola.
El campo del dipolo se calcula bajo la aproximación que la distancia entre las cargas, d, es mucho más pequeña que la distancia a la que estemos calculando el campo eléctrico. Es decir d<< x,z. Esta es la hipótesis fundamental. Al realizar estas las aproximaciones en el cálculo del campo eléctrico, vamos a quedarnos con los términos dominantes (más grandes), cómo se hizo hasta las últimas ecuaciones de la solución.
Como ejemplo, tomemos el primer término:
Intuitivamente vemos que en el caso que z>>d,x (asumo esto respecto a x para darle claridad al desarrollo) el segundo paréntesis nos queda algo como
Si multiplicamos por el término del primer paréntesis, tenemos
El primer término, z, es el más grande. La competencia entre el segundo y tercero está establecida por el factor (d/z) que multiplica al tercero y que hace al tercer término mucho más chico que el segundo. Por eso se despreciamos el término con d^2.
Dejo para que lo hagas con todos los términos como aparece en la solución.
Cualquier duda a las órdenes.
Entendí perfecto, muchas gracias!!
El mié., 18 de marzo de 2020 15:43, Juan Andres Muniz (vía FING) <
El mié., 18 de marzo de 2020 15:43, Juan Andres Muniz (vía FING) <