Tengo dudas de como razonar la demostración de este ejercicio, ¿Algún consejo?

La condición T3=T permite probar que λ3=λ (considerando un vector propio asociado), luego λ puede ser alguno de los siguientes: -1,0,1. Luego, λ1 =-1 y probar que un vector w está en el subespacio propio asociado al valor propio -1 es probar que T(w)=-w.
Se entiende?
Saludos,
Florencia.
Entiendo lo que me explicaste y pude hacer las primeras partes correctamente, pero no estoy seguro de como probar con que esa suma de transformaciones pertenece a ese subespacio y no a otro.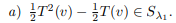
Debes aplicarle T al vector w= 1/2·T2(v)-1/2·T(v) y observar que te da -w, es decir,
T(1/2·T2(v)-1/2·T(v)) = - (1/2·T2(v)-1/2·T(v)),
será útil la identidad T3=T.
Saludos,
Florencia.