General

De forma más práctica, se me ocurre lo siguiente. Por ejemplo, dado el siguiente grafo:

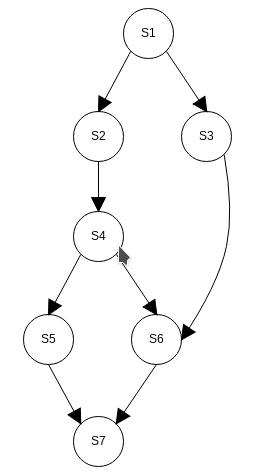
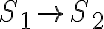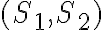podemos usar una flecha $S_1\rightarrow S_2$ para representar la ejecución secuencial (lo que vendría a ser el operador $S$ del libro) y $(S_1, S_2)$ para la ejecución concurrente (lo que vendría a ser el operador 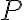$P$). Entonces uno empieza a hacer la traducción:

$\begin{align*} S_1\\ S_1\rightarrow (S_2,S_3)\\ S_1\rightarrow (S_2\rightarrow S_4, S_3\rightarrow S_6)\\ S_1\rightarrow (S_2\rightarrow S_4\rightarrow (S_5,S_6), S_3\rightarrow S_6\rightarrow S_7)\\ S_1\rightarrow (S_2\rightarrow S_4\rightarrow (S_5\rightarrow S_7,S_6\rightarrow S_7), S_3\rightarrow S_6\rightarrow S_7) \end{align*}$

Una vez que se ha llegado a desarrollar en profundidad todas las ramas, empieza a simplificarse con la regla de que si en un paréntesis está la misma tarea al final, puede "extraerse" para afuera. O sea, 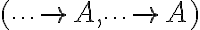$(\cdots \rightarrow A, \cdots \rightarrow A)$ se simplifica a 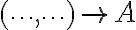$(\cdots,\cdots)\rightarrow A$. Esta simplificación empieza a hacerse desde el paréntesis más interno:

$\begin{align*} S_1\rightarrow (S_2\rightarrow S_4\rightarrow (S_5\rightarrow S_7,S_6\rightarrow S_7), S_3\rightarrow S_6\rightarrow S_7) \\ S_1\rightarrow (S_2\rightarrow S_4\rightarrow (S_5,S_6) \rightarrow S_7, S_3\rightarrow S_6\rightarrow S_7) \\ S_1\rightarrow (S_2\rightarrow S_4\rightarrow (S_5,S_6), S_3\rightarrow S_6) \rightarrow S_7 \end{align*}$

En este punto, no puede simplificarse más. Se ha llegado, en cierto modo, a una expresión "canónica" del grafo. Si en esta expresión reducida hay una etiqueta que aparece más de una vez, el grafo no es representable mediante cobegin-coend. En este ejemplo, aparece 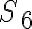$S_6$ dos veces por lo que no es representable mediante cobegin-coend.