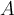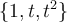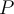Si me pueden ayudar con este ejercicio les agradezco, no dimos cambio de base cuando curse gal1 y no tengo ni idea como hacerlo, y si no es con cambio de base preciso ayuda igual, gracias!
Nicolás, hemos dado repasos sobre cambio de base tanto en el teórico como en los prácticos del semestre en curso. También tienes todo el material disponible para repasar.
Atenderé también tu duda a continuación, pero es importante que revises las clases o el material.
Las matrices de cambio de bases dentro de un mismo espacio vectorial, digamos V, no son otra cosa que matrices asociadas a la transformación lineal identidad id_V : V -> V. Trabajemos con la parte 1. del Ejercicio 9, por ejemplo. Te dan un vector genérico de R^3, llamado v, que lo puedes escribir como v = (x,y,z) donde x, y, z son números reales. coord_A(v) son las coordenadas de v en la base A, es decir coord_A(v) = (a,b,c), donde a, b y c son números reales que satisfacen la igualdad (x,y,z) = a (1,1,0) + b (1,0,1) + c (0,1,1) (tienes que usar en orden en el que aparecen los vectores en la base A). La idea es hallar quiénes son a, b y c. Esto se reduce a resolver la igualdad anterior, es decir, (x,y,z) = (a + b, a + c, b + c), o equivalentemente, debes resolver un sistema de ecuaciones dado por a + b = x, a + c = y, b + c = z. Ten en cuenta que nuestras variables son solamente a, b y c, mientras que x, y, z son números reales fijos. Entonces, cuando halles la solución a este sistema (con cualquiera de las técnicas que viste en GAL1), a, b y c van a depender de x, y, z.
De manera similar, puedes calcular coord_B(v).
Ahora, para hallar la matriz de cambio de base de la base B a la base A, hacemos lo siguiente:
1.) Calculamos coord_A((1,0,1)), es decir, las coordenadas del primer vector de la base B en la base A.
2.) Calculamos coord_A((0,1,0)).
3.) Calculamos coord_A((-1,0,1)).
4.) Colocamos los vectores anteriores como columnas para formar la matriz de cambio de la base B a la base A, es decir, A_((I))_B = (coord_A((1,0,1)) coord_A((0,1,0)) coord_A((-1,0,1))).
Eso sería todo. La otra matriz de cambio de bases la encuentras con el mismo procedimiento. Al final lo que te quedaría es verificar si tus cálculos son correctos por medio de la parte 3 del ejercicio.
Espero que la explicación te pueda ayudar.
Saludos,
Marco
Tienes que tomar un polinomio cualquiera
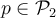 y expresarlo como c.l. de la base. Los escalares de esa c.l. son las coordenadas, que dependen del polinomio. Por ejemplo, como bien dices la base A es la canónica por tanto el polinomio
y expresarlo como c.l. de la base. Los escalares de esa c.l. son las coordenadas, que dependen del polinomio. Por ejemplo, como bien dices la base A es la canónica por tanto el polinomio 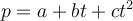 tiene como vector de coordenadas
tiene como vector de coordenadas 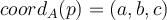 . Si la base no es la canónica hay que hacer más cuentas, que son las que están descritas en la respuesta de Marco.
. Si la base no es la canónica hay que hacer más cuentas, que son las que están descritas en la respuesta de Marco.