Hola gente, estoy haciendo un ejercicio que tiene un Karnaugh de 5 variables (problema 2, examen del 22/12/2016) y obtuve 2 diagramas para una salida. Van las imágenes adjuntas.
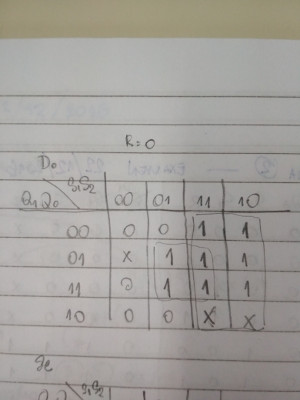
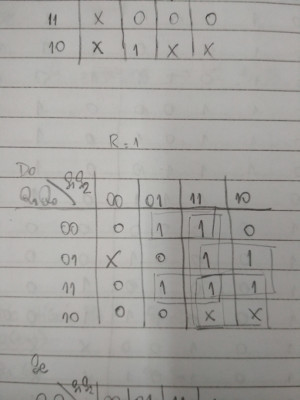
Las entradas son Q0, Q1, S1, S2 y R. Elegí usar la variable R para "separar" los diagramas y entonces hice lo que aparece en las figuras. Para cada diagrama hice los grupos de 1s (y algunas veces incluyendo X) de tamaño máximo.
Al momento de solapar los diagramas para obtener los factores de la ecuación de la salida D0 me fijé si en ambos diagramas había y en las mismas posiciones había 1 o X, y si así lo fuera, entonces yo creaba un grupo de 1s tal que le correspondiera un factor sin la entrada R.
Por ejemplo, para R=0 hay un grupo de 4 1s bien en el centro del diagrama, sin embargo, en el diagrama para R=1 no hay un grupo de elementos que correspondan. Falta un 1 o X en la posición 0101 del diagrama para R=1.
Por lo tanto, en ese caso tengo el factor Q0S2R' (R' es la R negada).
Ya en el caso del grupo (para R=1) que tiene 2 1s y 2 Xs sí hay un grupo en el otro diagrama (R=0) que tiene 1s o Xs en las mismas posiciones. O sea en ambos diagramas en las posiciones 1111, 1110, 1011 y 1011 hay 1s o Xs (bueno, hay que haber al menos un 1 porque grupos de Xs solamente no sirve).
Entonces, en ese caso tengo el factor Q1S1 (sin R porque al pasar de un diagrama a otro la R cambia de valor y entonces la variable no aparece en el factor de la ecuación de salida).
Resumiendo, ¿está bien ese razonamiento?
Saludos y gracias.
