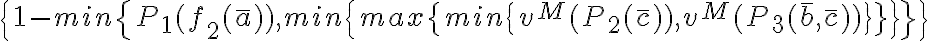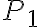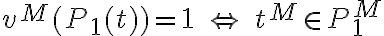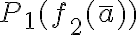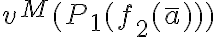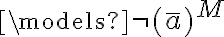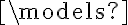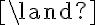[Ejercicio 8 a]

[Ejercicio 8 a]

de Alejandro Jose Rojas Quartino -
Número de respuestas: 3

Buenas, tengo una duda con este ejercicio. Se pide, para la estructura 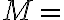M= (donde 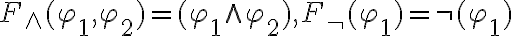F_{\wedge}(\varphi_{1},\varphi_{2}) =(\varphi_{1} \wedge \varphi_{2}), F_{\neg}(\varphi_{1})=\neg(\varphi_{1})) ver si se cumple 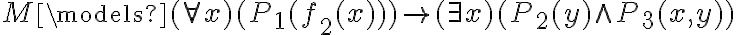M \models (\forall x)(P_{1} ( f_{2}(x) ) ) \rightarrow (\exists x)(P_{2}(y) \wedge P_{3}(x,y)) justificando.

Luego de desarrollar (usando la definición de 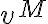v^{M}) llegué a esto:

\{ 1 - min \{ P_{1}(f_{2}(\overline{a})) , min\{ max \{ min \{ v^{M}(P_{2}(\overline{c})) , v^{M}(P_{3}(\overline{b} , \overline{c} )) \} \} \} \} \}

Mas allá de que las cuentas estén bien para llegar a esta expresión, lo que no me doy cuenta es como seguir.

No me doy cuenta como interpretar los predicados.

Muchas gracias desde ya, saludos!
En respuesta a Alejandro Jose Rojas Quartino

Re: [Ejercicio 8 a]

de Camila Sanz -

Hola,

Para el caso de P_1, por ejemplo, definimos la interpretación como: v^M(P_1(t)) = 1\ \Leftrightarrow \ t^M \in P_1^M .

En este caso tenés que interpretar P_1(f_2(\bar a)), para eso deberías mirar el valor de v^M(P_1(f_2(\bar a))) , es decir si el término interpretado en la estructura pertenece a la relación interpretada en la estructura.

En este caso cuál es la relación interpretada en la estructura? y el término interpretado en la estructura?


Saludos!
En respuesta a Camila Sanz

Re: [Ejercicio 8 a]

de Alejandro Jose Rojas Quartino -

Sería \models \neg (\overline{a})^{M} ??
En respuesta a Alejandro Jose Rojas Quartino

Re: [Ejercicio 8 a]

de Fernando Carpani -

Hola.

Yo tengo una pregunta.... de qué \models estás hablando? porque hay dos... al igual que hay dos \land y \neg ...

Un camino que puede ayudar a ver a donde conviene ir es interpretar "en lenguaje natural" lo que nos dice la fórmula y ver si tiene sentido con la realidad.

Saludos

FDO.