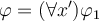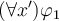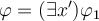Buenas noches, quisiera saber si el siguiente razonamiento es correcto para la resolución del ejercicio 8 parte a.
Sean 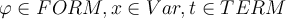 , se pide probar si la afirmación
, se pide probar si la afirmación  es libre para
es libre para  en
en 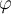 es verdadera o falsa, justificando en cualquier caso.
es verdadera o falsa, justificando en cualquier caso.
Pensé hacer inducción en 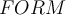 , la cual quedó (medio resumida, obviando algunos pasos) de la siguiente manera:
, la cual quedó (medio resumida, obviando algunos pasos) de la siguiente manera:
Se quiere probar la propiedad 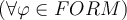 (
( esta libre para
esta libre para  en
en 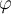 )
)
PB: 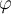 es atómica (o bien
es atómica (o bien 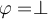 , o bien
, o bien 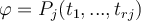 , o bien
, o bien 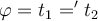 ).
).
Dem: Aplicando def de término libre para variable en una fórmula, como 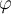 es atómica, entonces se cumple.
es atómica, entonces se cumple.
PI_1:
HI_1:  esta libre para
esta libre para  en
en 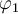 y
y  esta libre para
esta libre para  en
en 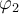
Dem: Por def de termino libre para una variable en una formula,  esta libre para
esta libre para  en
en 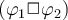 si
si  esta libre para
esta libre para  en
en 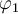 y
y  esta libre para
esta libre para  en
en 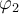 , lo cual es cierto por HI_1.
, lo cual es cierto por HI_1.
PI_2:
Dem:
Por def de termino libre para una variable en una formula,  esta
libre para
esta
libre para  en
en 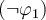 si
si  esta libre
para
esta libre
para  en
en 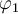 , lo cual es cierto por HI_2.
, lo cual es cierto por HI_2.
Dem:
Si 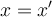 , entonces
, entonces 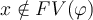 , por lo tanto es libre para
, por lo tanto es libre para  en
en 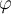 por definición de.
por definición de.
Si 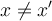 , entonces
, entonces 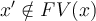 y
y  esta libre para
esta libre para 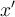 en
en 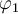 por HI_3.
por HI_3.
Aplicando el PIP en 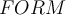 , concluyo que
, concluyo que  es libre para
es libre para  en
en 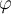 para toda
para toda 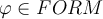 .
.
Saludos!