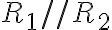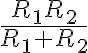Soluciones Práctico 9

Soluciones Práctico 9

de Maria Stefani Borrell Pombo -
Número de respuestas: 1
Como subieron las soluciones me pareció bueno comentar mis diferencias, acá están:

Ej 4
Parte a)
fmax/fmin = (Cmax/Cmin)1/2 = 36,51/2 = 6,04 
No entiendo la diferencia con el resultado colgado pues es una cuenta sencilla.
Parte b)
Sea a = fmax/fmin, con las nuevas frecuencias máxima y mínima.
Como el capacitor C2 se conecta en paralelo, voy a usar las capacidades máxima equivalente y mínima equivalente.
Entonces a = (C2+Cmax/C2+Cmin)1/2. Luego C2 = (a2Cmin-Cmax)/(1-a2) = 35,6 pF
Vuelvo a tener un resultado distinto.
Parte c)
Como fmin = 1/[2pi.L1/2(C2+Cmax)1/2], L = 1/[(2pi.fmin)2(C2+Cmax)] = 0,22 mH
Nuevamente no coincide, además me surge la pregunta... L no tendría que dar lo mismo si usara fmax y Cmin??

Ej 6
Parte a)
iM=femM/(Lw)= 5,22 kA
Parte c) i=4,35 kA. Arrastro diferencia

Ej 1A
Supongo que quedó mal escrita la solución, de todos modos a mi me dió:
iR(t)=[E/(R+R0)].[e-RRot/[L(R+Ro)]]


Agradezco que comenten! Saludos!
En respuesta a Maria Stefani Borrell Pombo

Re: Soluciones Práctico 9

de Pablo Iturralde -
Stefani,

En el ejercicio 4 tenés razón en las partes a) y c), había un número mal en nuestra solución que se arrastra. La parte b) era una cuestión de redondeo. Es correcto lo que decís de que L tiene que ser igual si lo calculas con los otros valores de C y f.

En el ejercicio 6 volvés a tener razón. La parte a) ya la habíamos corregido por sugerencia de otro compañero, pero nos había quedado la c) sin corregir.

En el ej. 1A la solución es exactamente la que vos planteás. Posiblemente el tema sea la notación: R_1 // R_2 denota el paralelo de dichas resistencias, lo que equivale a \frac{R_1 R_2}{R_1+R_2}.

Saludos,
Pablo.