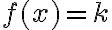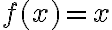Cálculo 1 anual
Perfilado de sección
-
- 3-8 Trabajamos la definición de límite para las funciones
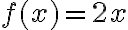 y
y 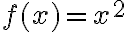 . Propiedades algebraica de los limites. (ver ejercicio 5)
. Propiedades algebraica de los limites. (ver ejercicio 5)
- 6-8: Ejemplos de no existencia usando la definición con la función
 . Limites laterales.Condición necesaria y suficiente de existencia de limites. Ejemplo con
. Limites laterales.Condición necesaria y suficiente de existencia de limites. Ejemplo con 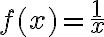
- 8-8:Estudiamos la función
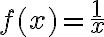 y probamos que
y probamos que  no tiene limite finito cuando
no tiene limite finito cuando  tiende a
tiende a  . Definimos limite infinito para
. Definimos limite infinito para  tendiendo a
tendiendo a 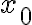 . Probamos que si
. Probamos que si 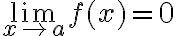 y
y  es acotada entonces
es acotada entonces 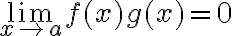 .
.
- 13-8: Definimos continuidad de una función en un punto y definimos función continua en su dominio. Mostramos que la funciones constantes y la función identidad son continuas. Propiedades algebraicas de las funciones continuas. Mostramos que suma de continua es continua. Trabajamos con funciones con discontinuidades:
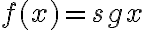 ,
, ![f(x)=[x] f(x)=[x]](https://eva.fing.edu.uy/filter/tex/pix.php/d0a42349646d7ba0cdb154e28162cb95.gif) ycon la función de Dirichlet.
ycon la función de Dirichlet.
- 15-8: Probamos que el lìmite del producto es el producto del limite y con elllo deducimos que producto de funciones continuas es continuo. Empezamos a trabajar con composiciòn de funciones continuas.
- 18-8: Probamos que la composicion de continuas es continua. Mostramos propiedades de monotonía de límite. Demostramos el teorema del sandwiche.
- 20-8: Teorema de conservación del signo. Enunciado del Teorema de Bolzano. Aplicaciones del teorema de Bolzano: Darboux, punto fijo, imagen de un intervalo por una función continua es un intervalo.
------------------------------------------------Hasta esta clase es lo que va para PRUEBA 7--------------------------------------------------------------
- 24-8 Demostración de Bolzano
- 27-8: Teorema de Weiestrass.
- 29-8: Continuidad de la función acumulativa de área. Función logaritmo es continua.
- 31-8: Funciones inversas y continuidad. Continuidad de la exponencial y de las raíces n-esimas
- 31-8: Funciones trigonométricas. Propiedades, Continuidad. Continuidad de funciones trigonométricas inversas. (CLASE EXTRA)
- 3-9: Funciones uniformemente continuas. Definición. Ejemplos: la función identidad y la funciones constantes. Demostramos que las funciones uniformemente continuas son continuas. Ejemplos:
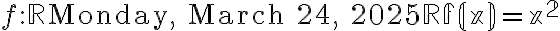 no es uniformente continua pero
no es uniformente continua pero ![f:[0,1]\to \mathbb R f(x)=x^2 f:[0,1]\to \mathbb R f(x)=x^2](https://eva.fing.edu.uy/filter/tex/pix.php/608e3bb13e38d3cf294fdaf3692a1a55.gif) es uniformemente continua. La función
es uniformemente continua. La función 
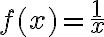 no es uniformemente continua. Enucianamos el teorema de Heine-Cantor.
no es uniformemente continua. Enucianamos el teorema de Heine-Cantor.
- 5-9: Probamos el teorema de Heine -Cantor
- 7-9: Probamos que
![f:[a,b]\to\mathbb R f:[a,b]\to\mathbb R](https://eva.fing.edu.uy/filter/tex/pix.php/cb60513e30005f37df669488fd05e46e.gif) continua es integrable. Teorema del valor medio para integrales de funciones continuas.
continua es integrable. Teorema del valor medio para integrales de funciones continuas.
- 10-9: Definición de derivada. Varios ejemplos. Suma de derivables es derivable, etc
- 17-9: Derivada de un producto de funciones y derivada de cociente de funciones.
- 19-9: Regla de la cadena. Teorema de la función inversa.
SEMANA DE PARCIALES
1-10: Recta Tangente. Definición de extremos: máximos y mínimos relativos. Demostramos que si
 es derivable en
es derivable en  y tiene un extremo en
y tiene un extremo en 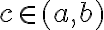 entonces
entonces 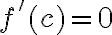 .
.3-10,5-10: Clases de consultas en el pizarrón
17-10 : Teorema de Rolle . Mostramos Lagrange como corolario de Rolle. Aplicaciones de Lagrange: signo de la derivada vs monotonía.
19-10: Clase de ejercicios sobre teorema de la derivada de la función inversa, extremos
24-10: TEOREMA FUNDAMENTAL DEL CALCULO. Regla de Barrow
26-10 ejercicios sobre TEOREMA FUNDAMENTAL DEL CALCULO. Regla de Barrow
29-10 Integración por partes
31-10 Integración por sustitución
5-11 Polinomio de taylor- definición.
- 3-8 Trabajamos la definición de límite para las funciones