Para poder sacar el not del modela:
- hay que tener una sentencia a la derecha (o sea, hay que clausurar primero si hace falta, no puede haber variables libres)
- aplica a toda la fórmula a la derecha del modela sí.
No, no es una distributiva del not.
Observar que 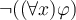 es lo mismo que
es lo mismo que 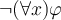 , cualquiera sea la fórmula
, cualquiera sea la fórmula 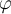 , ya que en el segundo caso simplemente se están simplificando los paréntesis.
, ya que en el segundo caso simplemente se están simplificando los paréntesis. 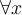 por sí solo no es una fórmula, no es nada, recién cobra sentido cuando tiene una fórmula a su derecha, a la cual cuantifica produciendo una nueva fórmula.
por sí solo no es una fórmula, no es nada, recién cobra sentido cuando tiene una fórmula a su derecha, a la cual cuantifica produciendo una nueva fórmula.
Las fórmulas siempre son como oraciones terminadas, con sentido. Por ejemplo 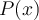 puede significar, en alguna estructura, "x es lindo/a" (o sea, P se corresponde con la relación "ser lindo/a").
puede significar, en alguna estructura, "x es lindo/a" (o sea, P se corresponde con la relación "ser lindo/a").
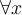 siempre significa "Para todo"/"Todo". Si alguien viene y dice "Para todo.", uno se queda esperando algo más "¿para todo qué?" "¿qué pasa con el 'para todo'?".
siempre significa "Para todo"/"Todo". Si alguien viene y dice "Para todo.", uno se queda esperando algo más "¿para todo qué?" "¿qué pasa con el 'para todo'?".
Justamente lo que estamos esperando es esa otra fórmula, "toda ciudad de Uruguay es linda" es una oración completa, que se formó a partir de la oración más simple "es linda" y se cuantificó. Por otro lado "toda ciudad de Uruguay" no está completa (ni siquiera es oración, no tiene verbo). ¿Se entiende?
Prestar atención a que la equivalencia no es "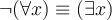 " sino "
" sino "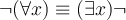 ", "no todos" es "hay alguno que no". ¿Queda claro eso? Es importante.
", "no todos" es "hay alguno que no". ¿Queda claro eso? Es importante.Cualquier duda volvé a consultar, no hay problema.
Saludos