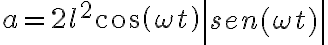 como
como 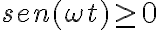 para
para ![t \in [0, \frac{ \pi}{2 \omega } ] t \in [0, \frac{ \pi}{2 \omega } ]](https://eva.fing.edu.uy/filter/tex/pix.php/5a27ff327378462d38473026b61c37a7.gif) se desprende que:
se desprende que: 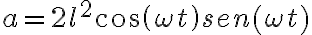 y por la formula que dan abajo esto deberia ser:
y por la formula que dan abajo esto deberia ser: 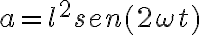 , en cambio en la solucion dice que
, en cambio en la solucion dice que 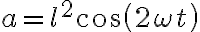 . Que es lo que está mal? Gracias.
. Que es lo que está mal? Gracias.
Estoy en la misma! Donde esta el error?
Hay errores en esa solución.
Tengan en cuenta que inicialmente el área es cero X(t=0)="ele" (igual a la arista del rombo) y que cuando comienza a crecer el tiempo, el área también lo hace aumentando el flujo magnético (en sentido positivo digamos, el del B).
Teniendo en cuenta ésto la corriente tendrá un sentido horario, ¿Ven por qué?
Cualquier cosa a las órdenes, suerte en eso!