Buenas, tenía una consulta con la parte b, antes de hacer una llamada recursiva el stack me quedó de la siguiente forma:
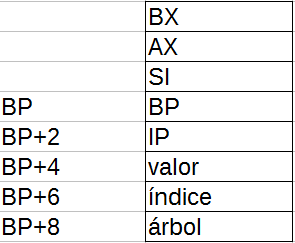
Entonces por cada llamada preciso lugar para 8 words a almacenar en el stack, hice la recursión,
buscarabb(0)=16
buscarabb(n)=16+buscarabb(n-1)
Entonces buscarabb(10)=16*11? o estoy contando una llamada de más?.
Con el tamaño del arreglo como cada elemento del árbol ocupa 2 bytes, si el árbol fuera completo:
cantbytes(abb)=2^(altura(abb)+1)bytes?
Es equivalente ver el peor caso con una lista que con un árbol completo para ver la cantidad de espacio necesario en el stack ya que toma va siempre hacia una rama sola?.
Si alguien tiene idea o ya lo hizo le agradezco.
Saludos