Lo que yo hice fue escribir una nueva funcion llamada 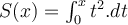
El problema que estoy teniendo con esta parte es que me confundo y no se asociar que seria f(x) en este ejercicio.
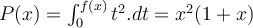
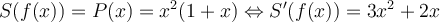
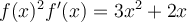
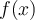

![\int_0^{f(2)}t^2\,dt=2^2(1+2)=12\Rightarrow \frac{f^3(2)}{3} = 12 \Rightarrow f(2)=\sqrt[3]{36} \int_0^{f(2)}t^2\,dt=2^2(1+2)=12\Rightarrow \frac{f^3(2)}{3} = 12 \Rightarrow f(2)=\sqrt[3]{36}](https://eva.fing.edu.uy/filter/tex/pix.php/150cc9890a8d13454d33643d73f52c7b.png)