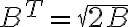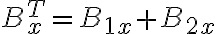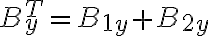hola puede alguien decirme como lo hizo para que le de como dice la letra porq a mi me queda todo igual solo que en ves de 2 tengo raiz de 2 y en vez de 4R^2 + D^2 tengo raiz de eso o sea yo lo que hize es halle el campo d euno de los conductores y el otro es igual. despues en el punto p lo que tengo es la suma vectorial de ambos entonces B tot = raiz de 2*B (porq los 2 son iguales y de ahi salen mis diferencias)
alguien podria decirme porq esto esta mal
gracias!!
Hola.
El problema es tomar
Esto es cierto solo si los vectores sumados son perpendiculares entre sí, además de tener el mismo módulo.
Tal vez no sea la forma más rápida para contestar el ejercicio, pero sugiero calcular las componentes horizontales y verticales de cada uno de los campos, y sumar componente a componente:
Saludos,
NC
Buenas gente, a mi tampoco me sale, yo llego a que el campo generado por uno de los conductores es Mu i d / 2pi*sqrt(d2+4R2). Está bien esto ?
De cualquier forma luego no se como llegar a la solución que me piden.
Gracias.
Por Ampère sabes que el campo generado por un conductor es B1=(Mu.i)/(2.pi.r) siendo r la distancia del eje del conductor a P. Lo mismo para el otro conductor, que genera B2.
Para sumar los campos y obtener lo que te piden hacelo componente a componente, ves que B1y y B2y se cancelan, por lo que queda sumar los B1x y B2x que tienen la misma dirección y sentido.
Luego B1x=B1.cosø siendo ø el ángulo formado por r y la recta que une a los conductores. Como cosø= d/(2.r) y r=[R2+(d/2)2]½, sustituís y llegaste a B1x. Ahora BP=B1x+B2x= 2.B1x ya que B1x y B2x tienen igual módulo.
Saludos