[Práctico 9][Ejercicio 6]

[Práctico 9][Ejercicio 6]

de Natalia Stephanie Pacheco Sosa -
Número de respuestas: 5

Buen día:


Con respecto a este ejercicio no entiendo como hacerlo. Por ejemplo en clases vimos como calcular integrales de algo que tiene raíz. Pero para que me sirve el dato pi???


Gracias.

En respuesta a Natalia Stephanie Pacheco Sosa

Re: [Práctico 9][Ejercicio 6]

de Pablo Mathias Perdomo Madruga -
Me parece que quieren que despejes de alguna forma las integrales para que te quede algo del estilo lo que te piden asumir.
En respuesta a Pablo Mathias Perdomo Madruga

Re: [Práctico 9][Ejercicio 6]

de Bernardo Marenco -

Buenas,

la idea es usar las propiedades de traslación y dilatación de la integral para llevar la integral que querés calcular a algo relacionado con la que te dan al principio. Por ejemplo, para la parte a) podés escribir:

\sqrt{9-t^2}=\sqrt{9\left(1-\frac{t^2}{9}\right)}=3\sqrt{1-\left(\frac{t}{3}\right)^2}

Entonces, si llamás 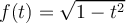f(t)=\sqrt{1-t^2}, eso último que llegamos lo podés ver como 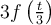3f\left(\frac{t}{3}\right), y podés usar la propiedad de dilatación para relacionar la integral de eso con la integral que te dan al comienzo.

Saludos,

Bernardo
En respuesta a Bernardo Marenco

Re: [Práctico 9][Ejercicio 6]

de Alberto Saul Garro Irurueta -

Otra forma es directamente aplicar a la expresión inicial la dilatación con 1/3.

\:\int _{-3}^3\:\sqrt{9-x^2}\:dx\:=3\int _{-1}^1\:\sqrt{9-\left(3x\right)^2}

=3\int _{-1}^1\sqrt{9\left(1-x^2\right)}\:dx

=3\int _{-1}^13\sqrt{\left(1-x^2\right)}\:dx

=9\int _{-1}^1\:\sqrt{1-x^2}dx

=\frac{9}{2}\pi


Saludos

Alberto