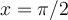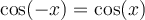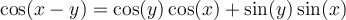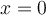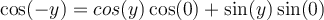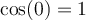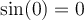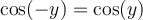Buenas tardes:
Tengo problemas a la hora de demostrar lo que nos piden dese el caso c) en adelante.
Lei las demostracines del libro pero no las entiendo. Porque si estas propiedades se cumplen para todo x e y,
a la hora de demostrar se toma casos especificos. Ejemplo toman y =pi/2 o x=0, cosas así. Cuál es la táctica para darme cuenta que
valores tomar.
Gracias.