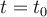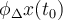Hola, según vimos en teórico, la potencia en modulación exponencial es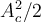 
. En la imagen que adjunto aparecen las cuentas que hice para querer demostrarlo pero no pude. Aparecen dos términos más que no se cómo seguir desarrollando. Para llegar al resultado estos deberían ser nulos. Si alguien sabe como hacerlo que cuente como hizo. Saludos!
Podes ver el desarrollo en el ejemplo 9.1-2 del Carlson.
En el desarrollo que planteas te conviene evaluar la E{\cos(...)} antes de hacer la última descomposición trigonométrica. Para esto planteas la expresión de la E{} en el caso de una VA continua con la integral del \cos que te va a dar 0.
Hola, gracias por la respuesta. Vi el ejemplo en el Carlson, pero resulta que en ese caso la función de probabilidad es una uniforme entre 0 y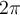 
lo que permite hacer explícitamente la cuenta, quedando claro porque da 0. No me queda claro que ocurre en el caso PM por ejemplo, donde no sabes cuál es la función de densidad del proceso 
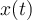. Pensando ejemplos se me ocurrió el de la foto donde tome otra función de densidad de probabilidad que cumple 
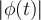. Llegué, luego de calcular la integral, a que no se anulaba dicho término. Seguramente me esté faltando alguna hipótesis sobre 
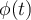donde la cuestión cerraría. Saludos!
No tiene que anularse en todos los casos. El caso de uniforme es el caso que nos incumbe, pues es el modelo que se hace de la señal y de la portadora. Es decir, la portadora no tiene que estar "sincronizada" de forma que tenga fase 0 para t=0, puede tener cualquier fase con igual probabilidad (por lo tanto uniforme).
O sea que fijando 
se asume que, por ejemplo en PM, 
tiene distribución uniforme?