Hola, tengo una duda sobre la solucion del primer problema del desarrollo. Una vez encontrado el potencial del campo, por que si hacemos la integral de linea de la parte c (circunferencia centrada en una carga) da cero? Si el campo fuese todo de gradientes esta claro que seria 0 al ser una curva cerrada, pero en este caso hay una singularidad dentro de la circunferencia. La solucion no estaria contradiciendo la ley de Gauss de F3? Capaz me es estoy confundiendo con algo simple y no me doy cuenta. Graciass
Lo que pasa es lo siguiente, que el dominio de un campo tenga agujeros no implica que una curva cerrada que rodee el agujero vaya a integrar distinto de 0, de hecho si dicho campo es de gradientes en ese dominio (como es el caso del ejercicio) va a integrar 0, porque al ser de gradientes vale la regla de Barrow para campos.
Lo que hay que tener claro es que si tenés un campo irrotacional y el dominio tiene agujeros (o sea, no es simplemente conexo), entonces PUEDE PASAR que sobre curvas cerradas que rodeen esos agujeros el campo no integre 0, pero no es necesario que pase siempre (cuando pase, el campo no será de gradientes en ese dominio). Es importante entender bien el teorema de equivalencia entre campos irrotacionales y de gradientes: ser irrotacional en un dominio simplemente conexo implica ser de gradientes, pero ser de gradientes implica solamente ser irrotacional, no implica que el dominio tenga que ser simplemente conexo (o sea, el teorema no te da un "sí y sólo sí", te da 2 afirmaciones por separado).
Para entenderlo más claro, el campo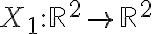
con 
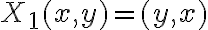es conservativo (ya que es gradiente de 
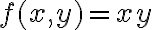), por lo tanto integra 0 sobre toda curva cerrada.
Si ahora considerás el campo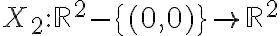
con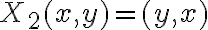 
, hiciste un agujero en el dominio del campo anterior (el origen), pero si integrás sobre una curva cerrada que rodee el origen va a seguir integrando 0 (hacerle un agujero al dominio no cambia el valor de las integrales porque las cuentas que tenés que hacer no cambian).
Lo que hay que tener claro es que si tenés un campo irrotacional y el dominio tiene agujeros (o sea, no es simplemente conexo), entonces PUEDE PASAR que sobre curvas cerradas que rodeen esos agujeros el campo no integre 0, pero no es necesario que pase siempre (cuando pase, el campo no será de gradientes en ese dominio). Es importante entender bien el teorema de equivalencia entre campos irrotacionales y de gradientes: ser irrotacional en un dominio simplemente conexo implica ser de gradientes, pero ser de gradientes implica solamente ser irrotacional, no implica que el dominio tenga que ser simplemente conexo (o sea, el teorema no te da un "sí y sólo sí", te da 2 afirmaciones por separado).
Para entenderlo más claro, el campo
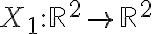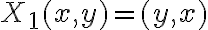con es conservativo (ya que es gradiente de 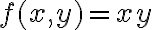), por lo tanto integra 0 sobre toda curva cerrada.Si ahora considerás el campo
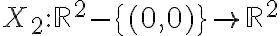con 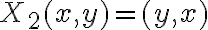, hiciste un agujero en el dominio del campo anterior (el origen), pero si integrás sobre una curva cerrada que rodee el origen va a seguir integrando 0 (hacerle un agujero al dominio no cambia el valor de las integrales porque las cuentas que tenés que hacer no cambian).Muchas gracias por responder, y entiendo lo que explicas pero en este ejercicio el "agujero" no es un punto cualquiera no? Es decir justo en ese punto se anula el denominador de la expresion del campo, sigue valiendo lo que me explicas con el campo X2? Y segun la ley de gauss hay una carga encerrada, por lo tanto la integral del campo no deberia ser cero no? Disculpa la molestia