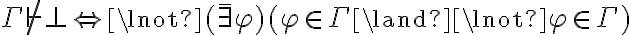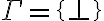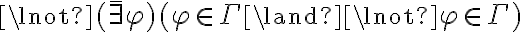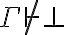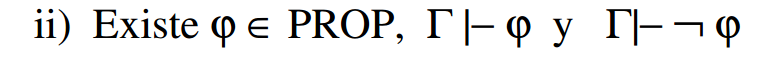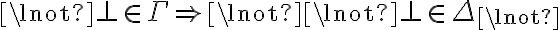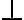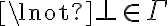La idea del ejercicio es, para cada parte, mostrar si lo que dice si es verdadero (dando una demostración) o falso (dando un contraejemplo, o una demostración) para cualquier conjunto infinito de fórmulas (esto porque se está tomando un 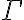 genérico con infinitas fórmulas). Si algún conjunto de fórmulas no lo cumple, entonces la afirmación va a ser falsa.
genérico con infinitas fórmulas). Si algún conjunto de fórmulas no lo cumple, entonces la afirmación va a ser falsa.
Es importante que en los verdadero/falso expliciten "Verdadero", "Falso", además de escribir la demostración o contraejemplo (porque no siempre se entiende qué es lo que están queriendo probar, y porque su respuesta está incompleta si no, ya que la letra lo pide expresamente "indique si es verdadero o falso, y justifique").
A las demostraciones le faltan justificaciones, y tienen algunos errores.
Tenés que explicitar cuando usás una definición o propiedad vista en el curso, por ejemplo:
![\Gamma \text{ es consistente} \Leftrightarrow \text{ [def consistencia] } \Gamma \not\vdash \bot \Gamma \text{ es consistente} \Leftrightarrow \text{ [def consistencia] } \Gamma \not\vdash \bot](https://eva.fing.edu.uy/filter/tex/pix.php/eb68d41ba0e319a0f51a98220a6f09a4.gif)
La siguiente línea está mal:
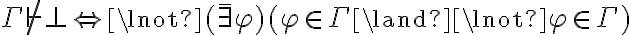
Contraejemplo:
Consideremos 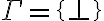
Se cumple que 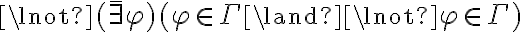
Pero no se cumple que 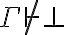 (por lema 1.5.3, si una fórmula pertenece a un conjunto, entonces el conjunto la deriva).
(por lema 1.5.3, si una fórmula pertenece a un conjunto, entonces el conjunto la deriva).
Creo que te estás confundiendo con el lema 1.6.3 o con el 1.6.9. Leelos cuidadosamente a ver si te das cuenta por qué es distinto a lo que vos pusiste.
En el ejercicio 2 también te falta justificar cómo pasas del primer renglón al segundo, del segundo al tercero (donde tenés un error similar al anterior), y no está completo, ¿no?
Creo que lo mejor sería que antes de escribir una demostración, analices bien a ver si estás entendiendo los enunciados, y te preguntes si es verdadero o falso. Luego tenés que justificar cuidadosamente cada paso, y si alguno no lo podés justificar, capaz que es porque está mal.
Algunos de los enunciados son falsos, por ejemplo el primero (con un contraejemplo simple, sale).
Trabajá un poco más los ejercicios y cualquier duda volvé a consultar.
Saludos



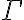
![\Gamma \text{ es consistente} \Leftrightarrow \text{ [def consistencia] } \Gamma \not\vdash \bot \Gamma \text{ es consistente} \Leftrightarrow \text{ [def consistencia] } \Gamma \not\vdash \bot](https://eva.fing.edu.uy/filter/tex/pix.php/eb68d41ba0e319a0f51a98220a6f09a4.gif)