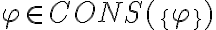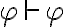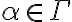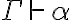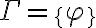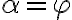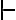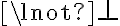Ej 4 parcial 2009

Ej 4 parcial 2009

de Nicolas Esteban Santos Reyes -
Número de respuestas: 2


Tengo una duda acerca de si esta afirmación es falsa o verdadera, por ejemplo me tomo dos teorías T1 y T2 tq T1={p0,cons(po)} y T2={p1,Cons(p1)} entonces creo que al hacer la intersección entre ellas me da vació efectivamente por lo tanto es falso ,pero como puedo demostrar que la intersección de dos conjuntos infinitos es vacía sin recurrir a la trivialidad.

Saludos.

En respuesta a Nicolas Esteban Santos Reyes

Re: Ej 4 parcial 2009

de Romina Romero - InCo -

Hola.

Un par de observaciones iniciales:

  • el CONS está definido para conjuntos, por tanto debemos poner llaves encerrando a p0 o p1: CONS({p0}), CONS({p1}).
  • Observar que una fórmula siempre pertenece a su CONS: \varphi \in CONS(\{\varphi \})
    • Dem:
\varphi \in CONS(\{\varphi \})
<=> def CONS
\varphi \vdash \varphi
y esto se cumple por lema 1.5.3 (si \alpha \in \Gamma entonces \Gamma \vdash \alpha , tomando \Gamma = \{ \varphi \} y \alpha = \varphi )

Por tanto, si bien tu conjunto igual está bien definido, sería mejor decir T1=CONS(po) y T2= CONS(p1).
(Además, observar que si hubieras escrito T1={p2,cons(po)} (o sea, si hubieras puesto otra fórmula afuera del CONS), esto no sería una teoría, porque p2 ^ p2 se deriva de T1, pero no está incluido en él, entonces T1 no sería teoría).

¿Qué hay en el CONS de un conjunto?
El CONS de un conjunto es el conjunto de fórmulas que se pueden derivar de él. Y, en particular, los teoremas se pueden derivar sin hipótesis, por tanto, también se pueden derivar de cualquier conjunto (repasar definifición de \vdash ). (En particular, se pueden derivar de T1, y también de T2). Como existen teoremas (por ejemplo \lnot \bot ), la intersección no es vacía, cualesquiera sean las dos teorías que se tomen.

Cualquier duda, consultá.

Saludos
Romina