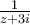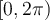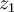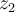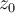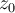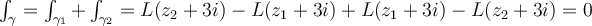Hola Gustavo
Lo que vos decis de calcular la integral con Cauchy está correcto. En ese momento no habíamos dado Cauchy todavía y el razonamiento de como calculamos la integral nos sirve para relacionar geométricamente esa integral con el índice de una curva respecto a un punto.
La función 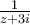 tiene primitiva en todo el plano menos una semirecta con origen en el -3i. En particular si definimos el logaritmo con argumento entre
tiene primitiva en todo el plano menos una semirecta con origen en el -3i. En particular si definimos el logaritmo con argumento entre 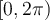 es la semirecta horizontal a la derecha de -3i (donde z-(-3i) tiene ángulo cero). La curva con la que estamos trabajando esta incluida donde
es la semirecta horizontal a la derecha de -3i (donde z-(-3i) tiene ángulo cero). La curva con la que estamos trabajando esta incluida donde 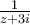 tiene primitiva. Entonces podemos aplicar la regla de Barrow y por ser una curva cerrada la integral da cero.
tiene primitiva. Entonces podemos aplicar la regla de Barrow y por ser una curva cerrada la integral da cero.
Si quisieras separarlo en dos curvas exactamente como en la otra integral, una de las curvas con punto inicial y final 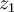 y
y 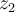 respectivamente y la otra al reves. Como en ambas curvas está definida la primitiva tendrías que:
respectivamente y la otra al reves. Como en ambas curvas está definida la primitiva tendrías que:

Si de una de las curvas hicieras tender su longitud a cero, esa curva tendería a un punto que llamemos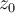 , esa integral te tendería a cero. Tendríamos entonces que:
, esa integral te tendería a cero. Tendríamos entonces que:

Como la función logaritmo es continua en 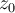 (
(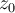 es un punto de la curva que no corta la semirecta donde el logaritmo no es continua) ese límite te da cero.
es un punto de la curva que no corta la semirecta donde el logaritmo no es continua) ese límite te da cero.
En la otra integral, como el logaritmo no era continuo en el punto que ahora llamamos 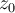 ese límite no nos daba cero.
ese límite no nos daba cero.
Se entendió?
Saludos!
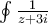 tiene primitiva y es una curva cerrada (por lo tanto da 0)
tiene primitiva y es una curva cerrada (por lo tanto da 0)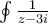 daba 2πi.
daba 2πi.