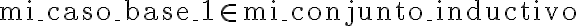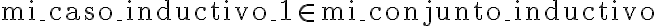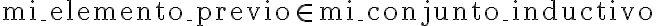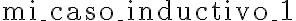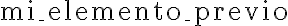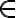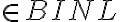Parciales

Tenés una idea cercana, pero estás mezclando algunas cosas.

Es correcta tu observación, estás dando una definición recursiva de una función, a la que llamaste BINL, que va de BIN en los naturales. ¿Qué es lo que hace tu función? Tu función está devolviendo el largo del binario - 1 (si le cambiamos el nombre de BINL a largo1 en tu definición, seguro tiene más pinta de función).

El conjunto que te piden son los pares <elemento del dominio, valor de tu función>.

Generalidades

• $\text{mi\_caso\_base\_1} \in \text{mi\_conjunto\_inductivo}$
  
• $\text{mi\_caso\_inductivo\_1} \in \text{mi\_conjunto\_inductivo}$ si $\text{mi\_elemento\_previo} \in \text{mi\_conjunto\_inductivo}$

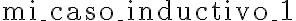Donde $\text{mi\_caso\_inductivo\_1}$ se construye a partir de 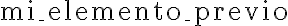$\text{mi\_elemento\_previo}$ haciéndole alguna cosa (en BIN, se le agregaba un 0 a la izquierda, por ejemplo). Además, esto ejemplifica 1 caso base y 1 caso inductivo, pero obviamente se podría extender a más (en el caso de BIN son 2 base y 2 inductivos).

Fundamental: si estoy definiendo un conjunto inductivo, tiene que aparecer el símbolo de 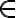$\in$.

En este ejercicio

Analicemos lo que nos piden:

BINL BIN x N, o sea que los elementos de BINL son también elementos de un producto cartesiano, por tanto, son tuplas de largo 2 <x,y>. La x tiene que estar en BIN, y la y es natural, pero además depende del largo de x. Y tengo que tener todos los elementos de BIN, entonces me voy a basar en su definición.

Borrador 1

• $\in BINL$
• $\in BINL$
• $\in BINL$ si $\in BINL$
• $\in BINL$ si $\in BINL$

¿Qué pongo en los _? ¿Cuál es el natural que le corresponde a cada uno?

Bueno, esto ya lo resolviste en tu función :). Eso sí, en vez de meter una función en la definición de BINL (además de la definición de la función ahora llamada largo1) y complicar las cosas, directamente usamos los valores:

Versión final

• $\in BINL$
• $\in BINL$
• $\in BINL$ si $\in BINL$
• $\in BINL$ si $\in BINL$

¿Se entendió? Cualquier duda consultá.

Saludos