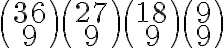Buenas, más que una duda es una comparación entre ese ejercicio y otro del grimaldi, que no estoy seguro si paso por alto algún detalle que los diferencie.
El ejercicio del practico dice esto; Ejercicio 8 a) >De cuantas maneras se puede particionar un conjunto de 6 elementos en subconjuntos de cardinal 3, 2 y 1 respectivamente? ¿Y si todos los conjuntos tienen cardinal 2?
Voy directamente a la pregunta "¿Y si todos los conjuntos tienen cardinal 2?" , la solución da 15, y sería así: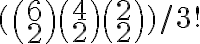 
Ahora este ejercicio del grimaldi: La maestra del ejemplo 1.20 debe formar cuatro equipos de voleibol, de nueve mujeres
cada uno, con las 36 estudiantes de primer año de su curso de educación física. ¿De cuántas
formas puede elegir esos cuatro equipos? Los equipos se llaman A, B, C y D.
En otras palabras, en el ejercicio del grimaldi, ¿No estoy particionado 36 elementos en 4 grupos de cardinal 9?
Solución del Grimaldi: 
La solución es con el mismo razonamiento, pero no lo divide sobre (4!), como en el ejercicio del practico lo hace sobre (3!), eso es lo que me confunde, ¿porque en uno divido el producto de las combinaciones, y en otro no?, si aparentan ser practicamente lo mismo.