Exámenes

Esto tiene que ver con la definición de estructura y de relación.

(¿Entendiste el universo?)

¿Qué es una estructura?

[def 2.2.1, resumida] <Conjunto ("universo"), Relaciones, Funciones, elementos distinguidos>

Observar que lo único que se le pide al conjunto universo es que no sea vacío, pero puede ser cualquier cosa. Personas, flores, palabras, números, símbolos como ●, etc.

¿Qué es una relación?

Acá vale una definición como la vista en discreta 1.

Una relación R_i, de los conjuntos A₁, A₂, ... , A_n es un subconjunto del producto cartesiano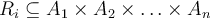
$R_i\subseteq A_1 \times A_2 \times \ldots \times A_n$

En nuestro caso, las relaciones son sobre A, entonces

$R_i\subseteq A ^ {algo}$

Donde algo es la aridad de R:

$R_i \subseteq A ^ {r_i}$

tal como dice la def 2.2.2.

Por tanto, las relaciones son conjuntos de tuplas, donde el largo de la tupla depende de la aridad de la relación y los componentes de la tupla son elementos del universo. Cuando algo cumple la relación es porque está en el conjunto, y cuando no la cumple es porque no lo está.

En el ejercicio de examen

El tipo de similaridad de la relación es 2 (relación binaria), o sea, es un conjunto (eventualmente vacío) de cosas de la forma

<algo₁, algo₂>, donde los algos tienen que ser elementos del universo.

El único algo disponible en el universo {●} es ●, así que la relación {<●,●>} es casi la única posible (¿cuál es la otra?).

Si la estructura fuera:

<{1}, {<1,1>}, {<1,1>}>

¿se ve más claro? Si es así, entonces la confusión pasa más bien por esperar que los conjuntos sean siempre numéricos, más que por la relación en sí. Y es importante que se abstraigan más y vean que esto de las estructuras sirve para modelar muchas más cosas que los números.

Espero que se haya entendido.

Saludos