ElecMag: Derivada de la energía y Fuerzas.

Tengo una duda general acerca de los ejercicios que tienen circuitos magnéticos y nos piden determinar una fuerza. En todos (o casi todos) tenemos un bobinado que está cortocircuitando, calculo que para mantener el flujo de B cte en el tiempo. El problema que tengo es que en varios ejercicios el flujo es una función de x (ya que cuando haces Hdl te queda la reactancia del vacio que depende de x), ahora ... para hallar la fuerza tengo que hacer 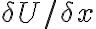$\delta U/ \delta x$ , siendo U = 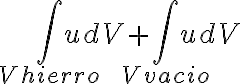$\int_{Vhierro}^{}{u dV} + \int_{Vvacio}^{}{u dV}$ , y en algunas soluciones de exámenes asumen, como B cte (en el tiempo), que 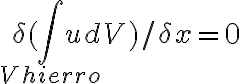$\delta ( \int_{Vhierro}^{}{udV} ) / \delta x = 0$ cosa que no entiendo porque B sigue siendo una función de x.

Esto lo hacen en la solución del ejercicio 3 del examen de Febrero 2013.

Saludos.

Re: Derivada de la energía y Fuerzas.

de Leopoldo Agorio - lunes, 21 de diciembre de 2015, 12:54

En ningún momento en la solución se formula una implicación entre constancia temporal y que dicha derivada sea nula.

Se trabaja con el bobinado en cortocircuito para mantener el flujo constante y que la fuerza se pueda calcular derivando la energía.

Fíjate que el procedimiento fue calcular la energía magnética y derivarla respecto a x para obtener la fuerza, como dices que hay que hacer.

Re: Derivada de la energía y Fuerzas.

de Diego Alonso Ruiz - lunes, 21 de diciembre de 2015, 13:50

me parece q lo quiso decir es que en la solucion calculan la derivada de la energía dejando el flujo como constante segun x, pero el flujo depende de x por una de las reluctancias (de hecho esta calculado un par de lineas mas arriba).

si no es eso lo q quiso decir, yo igual si tengo esa duda.

Re: Derivada de la energía y Fuerzas.

de Leopoldo Agorio - lunes, 21 de diciembre de 2015, 20:51

El flujo que se encuentre por el circuito magnético en t=0 se verá congelado al cortocircuitar el bobinado secundario.

Por otra parte, la fuerza (a flujo constante) se calcula realizando esa derivada parcial según x. La fuerza necesaria para que se cierre el entrehierro debe ser tal de anular la fuerza del resorte cuando x=0 que será kx0 (el estiramiento del resorte en dicha posición).

Es decir, se debe tener una corriente (en el instante inicial, porque luego el flujo se congela) capaz de generar una fuerza de esa magnitud.

Es decir, imponiendo dicha corriente en el instante inicial, cuando se cortocircuita el bobinado secundario, el entrehierro mide x0 y luego se cierra ya que la fuerza es kx0 hasta alcanzar el equilibrio, pero en todo este proceso el flujo se mantiene constante debido al bobinado en cortocircuito.