Buenas, tengo una duda con la parte b) de este ejercicio.
La parte a) me salio y supongo que la tengo que usar para la parte b), pero no se como... Lo que se me ocurre que como la letra te dice que hay que resolverlo por el principio de superposicion, por simetria el campo electrico en el centro de la cavidad generado por el contorno de la cavidad va a ser cero, porque el campo generado por un punto de la superficie de la cavidad se anula por otro que esta simetrico respecto el centro, esto es lo que no me cierra.. sin embargo el resultado es el mismo que la parte a), solo que en vez de r usa el vector a, por lo que trato de resolverlo de la misma manera que en a) pero no se como, porque cuando me tomo una superficie gaussiana, una esfera que pase por el centro de la cavidad, tengo una region sin carga, de la cual no se cuanto es su volumen para saber cuanta carga hay..
Bueno si alguien me puede decir como encararlo agradecido :)
Gracias!!
José,
me parece que estás encarando mal el ejercicio. La propuesta es de una esfera uniformemente cargada con densidad volumétrica de carga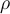 
. Esto implica que la esfera no es conductora.
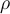. Esto implica que la esfera no es conductora. El principio de superposición que se propone es porque la situación total puede verse como una esfera de radio R uniformemente cargada menos otra esfera de un radio menor también uniformemente cargada.
No es cierto lo que decís que el campo generado por la esfera menor sea nulo. El campo generado por un punto en dicha esfera no se anula con el opuesto (excepto si estás considerando el campo en el centro de la esfera menor, que no es lo que se pide). De la misma manera que hiciste a) podés probar cuál es el campo generado por la esfera menor.
Te recomiendo que arranques por hacerte un buen dibujo de la situación, marcando bien los centros de ambas esferas y el punto P sobre el que estás queriendo calcular el campo.
Si te surgen más dudas (o no te saqué las que ya tenías) volvé a preguntar.
Saludos,
Pablo