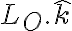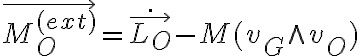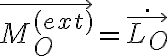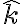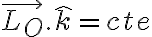Porque se puede afirmar que se conserva el momento angular segun k? Si hallo el momento segun k, me queda dependiendo de la derivada de phi y de sen2(tetha), lo que no pude demostrar que es constante. Pero se puede afirmar esto solo observando que la unica fuerza que no actua segun k es la componente del resorte que seria una fuerza central?
En respuesta a Agustin Iba
Re: Examen Febrero 2011 - Ejercicio 2
Hallas Lo, lo derivas y lo proyectas según k, si te da cero es porque se conserva según dicha dirección!
En respuesta a Gonzalo Daniel Martinez Gonzalez
Re: Examen Febrero 2011 - Ejercicio 2
de Agustin Iba -
bueno pero en este caso no da cero, queda dependiendo de theta y de phi. Por eso no sabia como comprobar que se conserva..
En respuesta a Agustin Iba
Re: Examen Febrero 2011 - Ejercicio 2
Derivas Lo y te queda según dos versores, que son ortogonales a k, y por eso al proyectarlo sobre k (haces producto interno) te queda cero.
En respuesta a Gonzalo Daniel Martinez Gonzalez
Re: Examen Febrero 2011 - Ejercicio 2
Sabes que entiendo perfectamente lo que vos decis pero, a mi el Lo segun k me queda Lo.k=4mL^2(senө)^2.φ'/3 y eso esta bien por q esta en la solucion, pero no entiendo por q cuando derivo esto da 0 supuestamnete , por q a mi no me queda , qe es lo q esta mal?
En respuesta a Erika Sonderegger Grieco
Re: Examen Febrero 2011 - Ejercicio 2
Sabés que yo quedé medio colgado con este tema desde el segundo parcial de 2010 (ejercicio2).
Ahí se conservan el momento y la energía, sin embargo cuando hallas sus expresiones, éstas están en función de ángulos variables en el tiempo.
A mi me parece coherente que el momento quede en función de theta y phi, lo que vos hallaste es la relación que deben cumplir estas dos variables en todo momento.
Sabiendo de antemano que se conserva el momento, el ejercicio es bastante fácil (digamos que es sólo cuentas...)
La duda que me quedó a mi es:
Si no estoy seguro si se conserva o no el momento, lo que podría hacer es hallar su expresión y derivarla; si al derivar me da cero, seguro se conserva. Pero si es un caso como éste??
Ahí se conservan el momento y la energía, sin embargo cuando hallas sus expresiones, éstas están en función de ángulos variables en el tiempo.
A mi me parece coherente que el momento quede en función de theta y phi, lo que vos hallaste es la relación que deben cumplir estas dos variables en todo momento.
Sabiendo de antemano que se conserva el momento, el ejercicio es bastante fácil (digamos que es sólo cuentas...)
La duda que me quedó a mi es:
Si no estoy seguro si se conserva o no el momento, lo que podría hacer es hallar su expresión y derivarla; si al derivar me da cero, seguro se conserva. Pero si es un caso como éste??
En respuesta a Erika Sonderegger Grieco
Re: Examen Febrero 2011 - Ejercicio 2
Es más fácil que eso, 
es constante porque la resultante de momentons externos es cero según esa dirección, acordate que 
, en este caso O es punto fijo, por lo que queda sólo 
, según la dirección de 
no hay ningúm momento externo, entonces 
, entonces 
es constante porque la resultante de momentons externos es cero según esa dirección, acordate que , en este caso O es punto fijo, por lo que queda sólo , según la dirección de no hay ningúm momento externo, entonces , entonces
Derivas el Lo según K, eso lo igualas a los momentos externos según K, como no tenes momentos externos según K, entonces lo que derivaste te queda igual a 0, entonces lo que derivaste es constante, allí vuelves para atrás y dices que Lo según K es constante por que su derivada es nula.
Capaz que se confunde lo siguiente, Lo segun K te puede quedar dependiendo de teta y phi o de lo que sea, pero eso es una parte de la igualdad, la otra parte son los momentos y como en K no hay, entonces te queda todo esa derivada igual 0, eso quiere decir que es constante.
Capaz que se confunde lo siguiente, Lo segun K te puede quedar dependiendo de teta y phi o de lo que sea, pero eso es una parte de la igualdad, la otra parte son los momentos y como en K no hay, entonces te queda todo esa derivada igual 0, eso quiere decir que es constante.
En respuesta a Bruno Carlo Giletti Cateura
Re: Examen Febrero 2011 - Ejercicio 2
Ahora si nos dio, gracias ;)