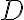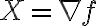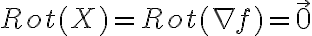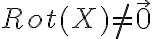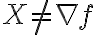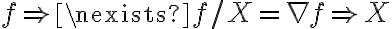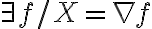Campo de gradientes

Campo de gradientes

de Maria Belen Corra Benia -
Número de respuestas: 3

Hola, una consulta, tengo el campo X (x, y)=(xy, xy). Cuando hago el rotor me da y-x, y el dominio es simplemente conexo porque es R2. Puedo decir que el campo no es de gradientes porque si x distinto de y el rotor no es cero, verdad? O esta mal?

Gracias!

En respuesta a Maria Belen Corra Benia

Re: Campo de gradientes

de Sebastian Passaro Pereira -

Está bien. Pensalo así:

X es de gradientes en un dominio D si X=\nabla f en D. Además, si esto se cumple, Rot(X)=Rot(\nabla f)=\vec{0}, la útlima igualdad se cumple siempre y se demuestra.


Entonces si Rot(X) \neq \vec{0}, es porque X\neq\nabla f para cualquier f \Rightarrow \nexists f / X=\nabla f \Rightarrow X no es de gradientes.
En respuesta a Sebastian Passaro Pereira

Re: Campo de gradientes

de Sebastian Passaro Pereira -
Si tuvieras que hacer una demostración formal no podés ovlidar que al principio es \exists f / X=\nabla f. Si te lo comes como yo y no están de humor capaz te comen algun punto.