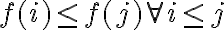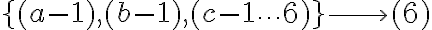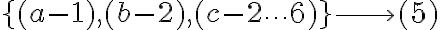Consultas generales

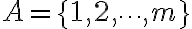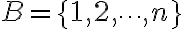Dados $A=\{1,2,\dots,m\}$ y $B=\{1,2,\dots,n\}$ calcular la cantidad de funciones f de A a B que satisfacen:

$f(i)\leq f(j) \forall i\leq j$ en A.

La respuesta dice que la cantidad de funciones es: 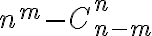$n^m-C_{n-m}^n$

Pongo un ejemplo en el cual el conjunto A tiene 3 elementos {a,b,c} y el B 6 elementos {1...6}. Según esa expresión habría 196 funciones, pero en mi ejemplo son 56. ¿En qué aspecto estoy pensando mal?

$\lbrace (a-1),(b-1),(c-1\dots6)\rbrace \longrightarrow (6)$
$\lbrace (a-1),(b-2),(c-2\dots6)\rbrace \longrightarrow (5)$

$\lbrace (a-1),(b-3),(c-3\dots6)\rbrace \longrightarrow (4)$

$\lbrace (a-1),(b-4),(c-4\dots6)\rbrace \longrightarrow (3)$

$\lbrace (a-1),(b-5),(c-5\dots6)\rbrace \longrightarrow (2)$

$\lbrace (a-1),(b-6),(c-6)\rbrace \;\;\;\;\;\;\; \longrightarrow (1)$

$\lbrace (a-2),(b-2\dots6),(c-2\dots6)\rbrace \longrightarrow 5+4+3+2+1$

$\lbrace (a-3),(b-3\dots6),(c-3\dots6)\rbrace \longrightarrow 4+3+2+1$

$\lbrace (a-4),(b-4\dots6),(c-4\dots6)\rbrace \longrightarrow 3+2+1$

$\lbrace (a-5),(b-5\dots6),(c-5\dots6)\rbrace \longrightarrow 2+1$

$\lbrace (a-6),(b-6),(c-6)\rbrace \;\;\;\;\;\;\;\;\;\;\;\;\;\;  \longrightarrow 1$

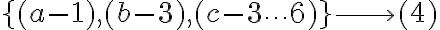
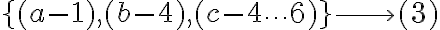
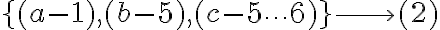
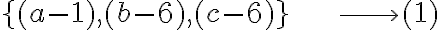
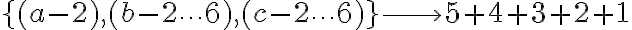
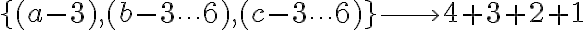
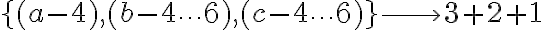
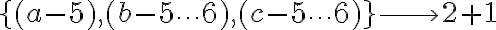
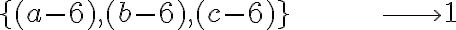
Total=56

Gracias.