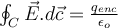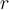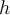Para la parte (a) que se pide el campo eléctrico en los puntos afuera del tubo conductor. No me queda claro la posible extensión del teorema de Gauss.
Si se toma una superficie cilíndrica que englobe el cilindro.
El problema es que generalmente, tenemos la estrategia de que el campo es constante, y puede "salir para afuera" de la integral, lo que facilita pila las cosas.

Mi pregunta es qué pasa en los "?", porque supongo que para el resto, puedo separar la integral en tres partes (dos tapas y el tronco).
Otras preguntas son:
- "de largo L" puede considerarse como infinito? En ese caso Gauss sigue sirviendo?
- La superficie cilíndrica (aunque luego se parta en varias integrales) el campo va a quedar dependiendo tanto del largo como del radio del cilindro. Eso choca con la pregunta anterior, porque si elijo un largo L, o 2L el valor del campo estaría cambiando pero si considero el cable muy largo. La distancia L no se considera infinita?
- Supongo que si el radio es igual al del cable no pasa nada, pero si lo aumento empieza a jugar los puntos en las zonas "?"
- En el caso de que elija largo L y radio igual al del cable, el campo queda expresado en función de ellos, y dónde estaría mi origen?, porque si es en una de las tapas, estoy diciendo que no siento campo eléctrico parándome en ella, sin embargo claramente lo hago.
- Volviendo a leer este post, me surgió otra duda. Si parto la integral en tres, los campos que despeje van a ser constantes pero distintos. La solución es como el campo en casos? "E = x si estoy parado al costado" etc
Saludos y gracias.