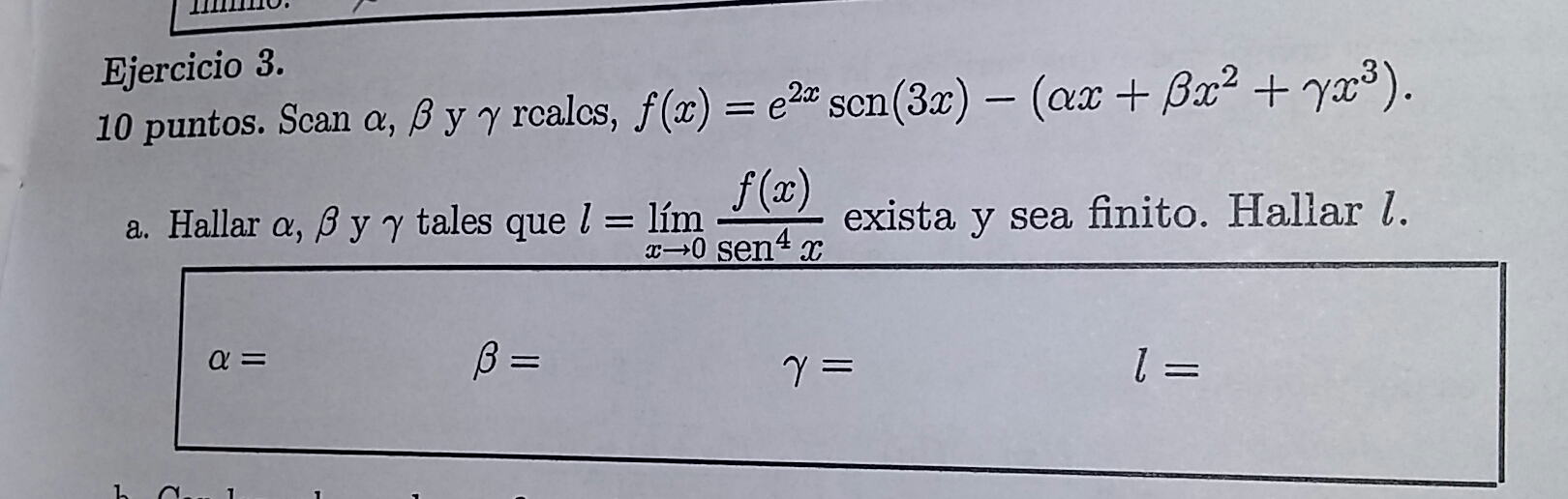Re: Ejercicio 3, examen 24 de febrero 2011
Hola Juan,
Este ejericio sale primero haciendo taylor hasta orden 4 en el punto 0 de e^3x.sen(2x) (tenès de hacer taylor de e^3x y luego el taylor de sen(3x) y luego los multiplicas dejando solo los tèrminos con grado menor o igual que 4)
Luego en el lìmite sustituìs e^ex.sen(3x) por ese desarrollo que hallaste, agrupàs los tèrminos en x, x^2, x^3 y x^4 y de ahì vas a sacar cuanto tiene que valer alfa, beta y gama para que el lìmite exista y sea finito. A su vez en el denominador tambièn debès hacer Taylor pero como el lìmite es tendiendo a 0, sabès que (sen(x)^4 equivale a x^4.
Entonces al final te va a quedar un lìmite donde vas a poder sacar fàcilmente cual es el valor de L.
Es medio engorroso de escribir, espero que te sirva.
Saludos.
Re: Ejercicio 3, examen 24 de febrero 2011
Buenisimo, lo habia hecho por Taylor yo tambien, pero lo que se me habia complicado era hacer el taylor de sen^4. Muchas gracias!! saludos