segundo parcial 2010 ejercicio 3

segundo parcial 2010 ejercicio 3

de Sarah Jun Morioka Machado -
Número de respuestas: 8
como se calcula el momento de inercia respecto al centro de la barra con las masas???
En respuesta a Sarah Jun Morioka Machado

Re: segundo parcial 2010 ejercicio 3

de Usuario eliminado -
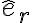Respecto al centro de masas del sistema (el punto medio de la barra), se calcula como siempre. El eje perpendicular a la hoja es principal porque la barra está contenida en el plano perpendicular, y el eje \hat e_r es principal por simetría.

Ahora cuánto valen tenés que aplicar la definición del tensor. Igual me parece que te queda:

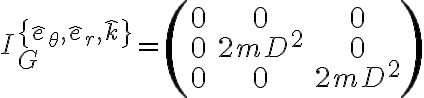I_G^{\{\hat e_\theta, \hat e_r, \hat k\}} = \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 2mD^2 & 0 \\ 0 & 0 & 2mD^2 \\ \end{array} \right) , con D la distancia de las masas al centro de la barra.



Después igual habría que usar Steiner para ver cuánto vale con respecto al centro del aro xD

Saludos, si me equivoqué corríjanme por favor :)
En respuesta a Usuario eliminado

Re: segundo parcial 2010 ejercicio 3

de Adriana Noelia Martinez Rodriguez -

una pregunta sobre este ejercicio...para sacar la ecuacion de movimiento yo calcule la expresion de la energia total del sistema, ya que se conserva puedo obtener directamente la expresion que piden pero me queda a menos de un dos dividiendo en el segundo termino, alguien sabe porque? si es que estoy aplicando algo mal o solo un error de cuantas?

gracias

En respuesta a Adriana Noelia Martinez Rodriguez

Re: segundo parcial 2010 ejercicio 3

de Usuario eliminado -
mmm... yo diría que no se conserva la energía. Si considerás sólo la barra y las 2 masas, hay una normal que trabaja (la perpendicular al plano). Y si considerás el aro también, no tengo ni idea pero el hecho de que gire a velocidad constante me hace pensar que alguien le está aportando energía al sistema.

Algún profe... please? :)
En respuesta a Usuario eliminado

Re: segundo parcial 2010 ejercicio 3

de German Suarez Granotich -
La energia no se conserva, el hecho de que el aro gire con velocidad constante te esta diciendo que hay una fuerza exterior actuando sobre el rigido entregandole o quitandole energia, por lo tanto decir que la energía se conserva está mal. Si en cambio el aro girara libremente ahi si se puede suponer que la energía se conserva.
En respuesta a German Suarez Granotich

Re: segundo parcial 2010 ejercicio 3

de Michael Varela Guglielmelli -
2010
Ej3 no puedo llegar a la ec. de movimiento
me quela la siguiente ecuación
(8)= angulo tita
no= angulo omega
Lo = I*w => Lo= {[(2m)*(Rsen(8)/2)2.k] +[(2m)*(R/2)2.j] } x {[n.k]+[d(8)/dt.j]}
=[no.mR2sen2(8)]/2 + [(mR2)(d(8)/dt)/2]=Lo

=> dL/dt = (mR2/2) [2sen(8)cos(8)(d(8)/dt)no + (d2(8)/dt2)] = (-mgRsen(8))/2

entonces despejando me queda:
d2(8)/dt2 + 2sen(8)cos(8)no(d(8)/dt) + 2gsen(8)/R =0
y esto no es la solucion que dice el parcial por favor si alguien me ayuda
disculpen no se escribir en latex
En respuesta a Michael Varela Guglielmelli

Re: segundo parcial 2010 ejercicio 3

de Maria Jose Varela Dipaola -

Consulta: la inercia del rígido vendría a ser la del aro mas la de las masas puntuales unidas no? porque no me está dando...me queda g.sen(theta)/3R en el último término de la ecuación de movimiento y es g.sen(theta)/2R.