En el ejercicio 2 del parcial del 23/6/10 te pide el flujo del rotor del campo X sobre determinada sup, pero el problema que me surgio fue que la letra te da dos campos X(x,y,1)=(y,-x, e^y + sen(x)) y X(x,y,4)=(y,-x, 6y+3x^2) y entonces no me doy cuenta como hallar el rotor de este campo.
Muchas gracias!
probablemente, lo que ocurre es que tengas que usar Stokes,
si me pasás la letra completa, vemos qué se puede hacer
saludos
jana
Hola, me surgió alguna duda con este ejercicio. Puede ser que si le sumas las tapas a la superficie, el flujo del rotor de la suma de esas tres superficies sea cero?
Lo consulte en el practico y el tema es la superficie, ya que sus bordes se dan en z=1 y z=4, entonces usas stokes dos veces con los diferentes campos que te da la letra, no se si me explique bien, espero que si! Saludos
No, no es así. Hay que usar Stokes.
Por Stokes, el flujo del rotor de X sobre S es igual a la circulación de X sobre el borde de S.
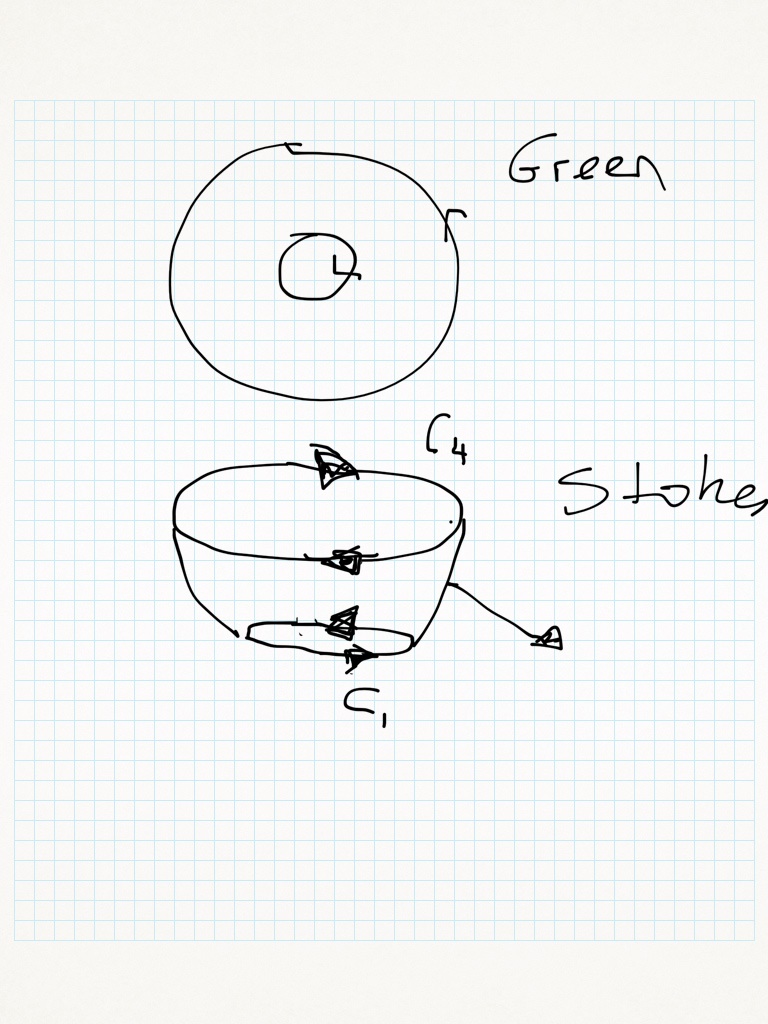
El borde de S consta de dos curvas: las circunferencias:
C1= (cost, sent, 1) y C4=(2cost, 2sent, 4)
la superficie está orientada con normal apuntando hacia abajo. Para que quede coherente con esta orientación, la curva "de afuera" tiene que ser C1 y la "de adentro" tiene que ser C4. Es decir
\int_S rot(X)dS = \int_C1 Xd\alpha -\int_C4 Xd\alpha
ahí es donde se usan las expresiones de X con valor en z=1 y z=4
la primera integral queda -2pi y la segunda 8pi. Si hice bien las cuentas, el flujo da entonces 6pi
Hola, no entendi por que restas las dos integrales. Yo calcule las 2 circulaciones por separado y me dieron 2pi y 8pi positivas las 2, y pienso que habria que sumarlas porque el borde de S es la union de las 2 cfas.
No, no es así, no se suman los dos bordes. En Green, hay un borde exterior que se recorre en sentido antihorario, y uno o varios bordes interiores, que se recorren en sentido horario. Lo mismo pasa con Stokes. Cuál es el sentido de las curvas lo determina la normal. En el ejemplo, si recuerdo bien, la curva que da 2pi es la exterior y la otra es la interior, por eso se debe recorrer en el otro sentido, y por lo tanto cambia de signo
saludos
jana
No me queda claro cual es la curva exterior y cual es la interior. En el caso de green en el plano me se dar cuenta, pero acá en R3 no
perdón, va de nuevo porque en el dibujo que mandé antes estaba exactamente al revés, mil disculpas
el recorrido de las curvas lo da la normal, según la regla de la mano derecha. Si el pulgar apunta a donde apunta la normal, la forma en que se cierra la mano derecha te da el recorrido de cada una de las curvas.
En el ejercicio, la normal apunta hacia abajo. La superficie es el pedazo de paraboloide entre z=1 y z=4.
Con esa normal apuntando hacia abajo, el recorrido de la curva C4 y el de la curva C1 es el que está en el dibujo que te adjunto, saludos
jana
pd: fijate si lo entendés, si no avisame, saludos
genial, saludos