Una pregunta

Re: Una pregunta

de Eleonora Catsigeras. -
Número de respuestas: 0
No sé a qué te referís, si podés poner un ejemplo tal vez me dé cuenta.

En general, la condición de Lipschitz para una función 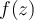f(z) definida en un abierto 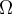\Omega es por definición que existe
una constante real 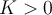K >0 tal que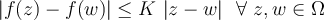
|f(z) - f(w)| \leq K \ |z-w| \ \ \forall \ z, w \in \Omega

Se puede demostrar que toda función que cumple la condición de Lipschitz es continua, pero el recíproco es falso.

Se puede demostrar que toda función holomorfa en 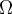\Omega que tenga derivada acotada en módulo, es Lipschitz, pero el recíproco es falso.

En el curso de ecuaciones diferenciales se ve el teorema de Picard, que tiene
como una de sus hipótesis que la función (en ese caso de variable real) que está en el segundo término de una ecuac. diferencial ordinaria de primer orden, cumple la condición de Lipschitz.