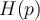 es la respuesta al escalón, es decir que
es la respuesta al escalón, es decir que  G(p)= L[s(t)](p)](https://eva.fing.edu.uy/filter/tex/pix.php/5d9514b89aa62473dc6dacca4ff02646.png) donde
donde 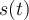 es la salida del sistema cuando la entrada
es la salida del sistema cuando la entrada 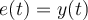 (siendo
(siendo 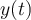 el escalón de Heaviside).
el escalón de Heaviside). Como el sistema es lineal sabemos que:
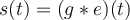
y también sabemos que transformando:
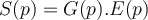
Ahora, si mi entrada es el escalón
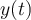 su transformada de Laplace es:
su transformada de Laplace es:=Y(p)= \frac {1}{p} L[y(t)](p)=Y(p)= \frac {1}{p}](https://eva.fing.edu.uy/filter/tex/pix.php/7c9a31433fc50b72421c751025ea1842.png)
Por lo que nos queda:
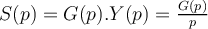
De donde yo deduzco que:
 \neq G(p) L[s(t)](p) \neq G(p)](https://eva.fing.edu.uy/filter/tex/pix.php/0b59654620e71a70f733cde3243fb0fd.png)
A mi me parece, no estoy 100% seguro, de que hay un error en la letra, creo que en todo sistema lineal la función de transferencia
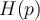 es la respuesta al impulso, es decir que
es la respuesta al impulso, es decir que  G(p)= L[s(t)](p)](https://eva.fing.edu.uy/filter/tex/pix.php/5d9514b89aa62473dc6dacca4ff02646.png) donde
donde 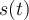 es la salida del sistema cuando la entrada
es la salida del sistema cuando la entrada 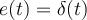 (siendo
(siendo 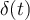 la distribución "Delta de Dirac"). Por lo siguiente:
la distribución "Delta de Dirac"). Por lo siguiente:Como el sistema es lineal sabemos que:
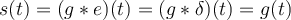
y también sabemos que transformando:
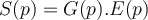
Como mi entrada es
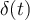 su transformada de Laplace es:
su transformada de Laplace es: =1 L[ \delta (t)](p)=1](https://eva.fing.edu.uy/filter/tex/pix.php/5b80fc09b417921f782ad3b9f744b149.png)
Nos queda:
= G(p) S(p)=G(p).L[ \delta (t)](p)= G(p)](https://eva.fing.edu.uy/filter/tex/pix.php/227212cf3255a8059f99554b57952ade.png)
Que es lo que pide probar. Si me estoy equivocando que alguien me corrija, porque la verdad me confundió bastante este ejercicio.
Saludos,
Martín
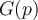
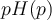
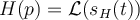
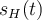
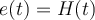
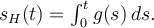
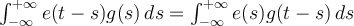
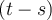
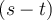
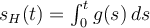
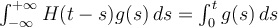
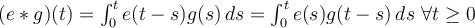
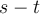
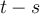
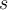
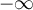
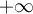
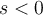
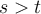
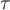
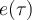
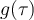
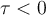
![[0,t] [0,t]](https://eva.fing.edu.uy/filter/tex/pix.php/3ce1e7c3f34fc9d85fa60a9345f7f5a5.png)