Claro,
Primero que nada te sugiero que tomes la norma que esta a la izquierda de la igualdad, luego apliques la definición de norma (raíz del producto interno), aplicas la distributiva (recordar que la norma de T es 1) y la identidad que relaciona el producto interno con la norma (es la que aparece el coseno del ángulo). Si todo va bien vas a obtener que la expresión de la izquierda elevada al cuadrado corresponde a:
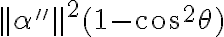 donde
donde  es el ángulo que forman los vectores
es el ángulo que forman los vectores 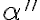 y
y 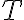 .
.
Por otro lado tomas la expresión que esta a la derecha y usas la identidad que relaciona la norma del producto vectorial con las normas de cada vector (aparece un seno del ángulo), allí obtendrás:
Por lo tanto ambas normas coinciden.
Saludos
Gabriel