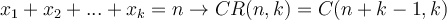¿Cuál es la forma más sencilla para contar las soluciones de una ecuación del tipo:
x1 + x2 + x3... = n
Tal que: 4<x1 < 6; 3< x2 <7 y así...?
Gracias!
Conteo de soluciones de una ecuación con condiciones.
Número de respuestas: 3
En respuesta a Bruno Sena Giuggiolini
Re: Conteo de soluciones de una ecuación con condiciones.
Combinas varias tecnicas por lo general. Por ejemplo, si te dicen x1 > 4, podes asegurar que x1 valga 4 (restas 4 del lado del lado derecho de la igualdad y quitas la condicion).
Para los casos en los que te digan por ejemplo x1 < 7, podes plantear la solucion general y luego buscar las soluciones con x1 >= 7, y vas haciendo asi para cada incognita.
Saludos.
Para los casos en los que te digan por ejemplo x1 < 7, podes plantear la solucion general y luego buscar las soluciones con x1 >= 7, y vas haciendo asi para cada incognita.
Saludos.
En respuesta a Hector Alberto Asencio Larrañaga
Re: Conteo de soluciones de una ecuación con condiciones.
La segunda parte se hace con combinaciones con repetición no? Muchas gracias!
En respuesta a Bruno Sena Giuggiolini
Re: Conteo de soluciones de una ecuación con condiciones.
En realidad, esas ecuaciones siempre se plantean con combinaciones con repeticion. En forma generica:
En el caso donde algun x tenga que ser al menos algun valor particular (por ejemplo, x1 = 3), simplemente lo restas a n y planteas la formula de combinaciones con repeticion. Cuando tenes que algun x tenga maximo, planteas por inclusion/exclusion.
En el caso donde algun x tenga que ser al menos algun valor particular (por ejemplo, x1 = 3), simplemente lo restas a n y planteas la formula de combinaciones con repeticion. Cuando tenes que algun x tenga maximo, planteas por inclusion/exclusion.