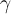Primer parcial 07/05/2011 Enunciados y soluciones

Re: Primer parcial 07/05/2011 Enunciados y soluciones

de Eleonora Catsigeras. -
Número de respuestas: 0
Había un error en las soluciones del ejercicio 2 parte a, el signo del índice de las curvas estaba mal en dos casos, en las vueltas de la curva \gamma :

Alrededor del punto 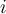i da una vuelta en sentido Horario y el signo entonces es NEGATIVO, Ind_ {\gamma} ( i ) = -1.

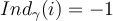Alrededor del punto 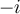- i da una vuelta en sentido Antihorario, y el signo entonces es POSITIVO Ind_ {\gamma} (- i ) = +1.

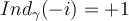El resultado final de la parte a del ejercicio 2 queda 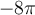- 8 \pi , y en las soluciones publicadas antes estaba mal el signo.

Ya corregimos el error en las soluciones. Muchas gracias por habernos avisado.

El desarrollo correcto en definitiva es este (espero no estar equivocándome de vuelta):

I=\int_{\gamma} f(z)\, dz = 2\pi i\, \cdot \left [2i \cdot Ind_{\gamma}(-i) - 2i\cdot Ind_{\gamma}( i) -i \cdot Ind_{\gamma}(-2i) +i\cdot Ind_{\gamma}(2i) \right ]=
= 2\pi i\, \cdot \left [2i \cdot (+1) - 2i\cdot (-1) -i\cdot (-1) +i\cdot (-1) \right ] = -8\pi.