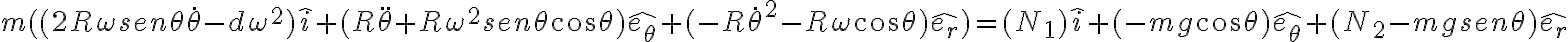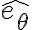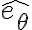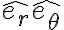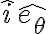Hola,
En la parte a luego de derivar la posición para encontrar la aceleración, hice "Newton" en la partícula.
No me queda claro del todo, por que, se plantea que hay que multiplicar por etita . Me queda claro si, que en esa dirección no hay reacciones "desconocidas", pero no visualizo por qué multiplicar por etita siendo que en la aceleración hay un término en etita.
Quizás hay algo respecto a los sistemas de referencia que estoy perdiendo de vista, pero sinceramente no me doy cuenta.
Saludos.