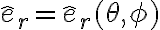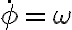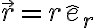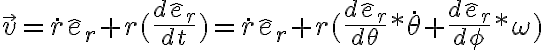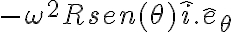Ej 1 primer parcial 2010

Ej 1 primer parcial 2010

de Ernesto Marchesoni Seijo -
Número de respuestas: 2
Hola gente, estoy intentando entender la solucion dada a este ejercicio. Asi que todo lo que planteo esta en base a esa solucion...

El tema es cuando busca la aceleración según eΘ:

a= R (d2Θ/dt) eΘ - R (dΘ/dt)2 er

(para empezar y a los ponchazos, mi respuesta serìa "el primer termino de la ec"... ya que er 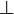\perp eΘ , asi que esto serìa otra duda...)

Pero sigo con la solucion... plantea esto:

a . eΘ = R (d2Θ/dt) - w2R senΘ i . eΘ

Esto me parece magia!!!... no entiendo como puede vincular (dΘ/dt) con w!!!!

Al senΘ lo explico como el er abatido sobre i, pero despues, magic!

Muchas gracias!
En respuesta a Ernesto Marchesoni Seijo

Re: Ej 1 primer parcial 2010

de Usuario eliminado -
No entiendo mucho lo que pusiste arriba, pero acordate que:

\hat e_r = \hat e_r(\theta,\phi), siendo \dot \phi = \omega.

Si la posición la escribís como:

\vec r = r \hat e_r, entonces la velocidad te queda:

\vec v = \dot r \hat e_r + r ( \frac{d\hat e_r}{dt}) = \dot r \hat e_r + r (\frac{d\hat e_r}{d\theta} * \dot \theta + \frac{d\hat e_r}{d\phi} * \omega)

Ahí te aparece el omega por primera vez y más veces cuando hacés la derivada segunda. Si no la otra manera es hacerlo por Coriolis, donde el término ese -\omega^2Rsen(\theta)\hat i . \hat e_\theta te aparece como el último término de la aceleración de transporte.

Espero q te haya servido (y espero no haberla pifiado =P). Saludos!