Esa fórmula se demuestra a partir del criterio de D'Alambert de convergencia
de series numéricas de términos positivos.
Escribo aquí abajo el enunciado y la demostración de la fórmula que escribió Alejandro para calcular el radio de convergencia:
Hipótesis (H): Se tiene una serie de potencias
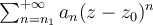 .------------ . (A)
.------------ . (A)tal que existe (real finito o
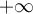 ) el límite siguiente:
) el límite siguiente: 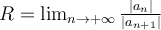 .------------- . (R)
.------------- . (R)Tesis (T):
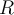 es el radio de convergencia de la serie de potencias (A).
es el radio de convergencia de la serie de potencias (A).Demostración:
Del curso de Cálculo 1, sabemos el criterio de D'Alambert, que dice esto:
Si
 . ---------. (B)
. ---------. (B)es una serie cuyos términos son números reales no negativos
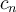 , y si existe (real o
, y si existe (real o 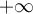 } el límite
} el límite 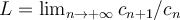
entonces:
-- Si
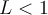 entonces la serie (B) converge.
entonces la serie (B) converge.-- Si
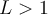 o si
o si  es
es 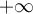 entonces la serie (B) diverge.
entonces la serie (B) diverge.-- Si
 este criterio de D'Alambert no afirma nada sobre la convergencia de la serie (B).
este criterio de D'Alambert no afirma nada sobre la convergencia de la serie (B).Bueno, ahora tomemos la serie (A), y definamos la serie auxiliar (B) usando
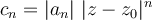 . -------------------. (C)
. -------------------. (C)(Observar que
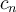 es real no negativo).
es real no negativo).Usando la hipótesis (H) de que existe (real o +\infty) el límite (R), observamos
que
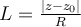 . ------------------------(D)
. ------------------------(D) ¿Se entiende esta igualdad (D)?. Sale de la definición de
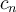 en la igualdad (C), para construir la serie auxiliar (B) como está dicho en el párrafo anterior, y de juntar el cálculo del límite según la igualdad (L), con la hipótesis (H) de que existe el límite según la igualdad (R).
en la igualdad (C), para construir la serie auxiliar (B) como está dicho en el párrafo anterior, y de juntar el cálculo del límite según la igualdad (L), con la hipótesis (H) de que existe el límite según la igualdad (R). Luego, aplicando el criterio de D'Alambert a la serie auxiliar (B) (que construimos a partir de la serie de potencias (A) dada en la hipótesis)
deducirmos que
-- la serie auxiliar (B) converge si
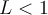 , o sea si
, o sea si 
--la serie auxiliar (B) diverge si
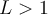 , o sea si
, o sea si 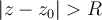
Ahora, observamos que la serie auxiliar (B) es la serie de módulos de la serie de potencias (A). Entonces, si converge la serie auxilar (B), por definición de convergencia absoluta, la serie de potencias (A) converge absolutamente. (esto es converge la serie de sus módulos).
El teorema que dice que la convergencia absoluta implica la convergencia , con su demostración, igualita, vale para series de términos complejos en vez de restringirse a términos reales. Solo hay que sustituir, en ese enunciado y su prueba, módulo donde decía valor absoluto.
Entonces deducimos que
-- la serie de potencias (A) converge si
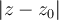 .------------- . ( I )
.------------- . ( I )-- la serie de potencias (A) no presenta convergencia absoluta si
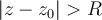 .------------- . ( II )
.------------- . ( II )Finalmente recordamos que el teorema de existencia de radio de convergencia de una serie de potencias cualesquiera, dice que o bien la serie converge para todo
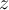 , en cuyo caso se dice que el radio de convergencia es
, en cuyo caso se dice que el radio de convergencia es 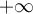 , o bien, existe un único número real
, o bien, existe un único número real  tal que:
tal que:-- la serie de potencias converge y converge absolutamente para todo z tal que
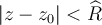
-- la serie de potencias no converge y no converge absolutamente para todo z tal que
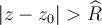
Por la unicidad del radio de convergencia, las afirmaciones ( I ) y ( II ) implican que el radio de convergencia
 de la serie de potencias (A) debe ser igual al número
de la serie de potencias (A) debe ser igual al número 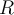 que aparece en las afirmaciones ( I ) y ( II ). Este número
que aparece en las afirmaciones ( I ) y ( II ). Este número 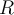 era el definido en la igualdad (R). Se terminó de probar entonces que el radio de convergencia de la serie (A) se puede calcular con la fórmula dada en la igualdad (R). LQQD.
era el definido en la igualdad (R). Se terminó de probar entonces que el radio de convergencia de la serie (A) se puede calcular con la fórmula dada en la igualdad (R). LQQD.Como agregado que me parece que hay que recordar, enuncio las tres siguientes "recetas", sobre la teoría de series. (Las dos primeras se demuestran en forma similar a lo visto en series de Cálculo 1, pero usando complejos y sus módulos en vez de reales y sus valores absolutos. La tercera se demuestra igual que a lo que no sé si vieron en el curso de Ecuaciones Diferenciales sobre series de potencias de funciones de variable real):
--una serie de términos complejos cualquiera converge si converge absolutamente (o sea si converge la serie de los módulos, que es una serie de reales no negativos)
--existen series de términos complejos que convergen pero que no convergen absolutamente
--si una serie de términos complejos es una serie de potencias centrada en
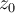 , que tiene radio de convergencia
, que tiene radio de convergencia 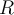 , y si el valor de la variable z es tal que
, y si el valor de la variable z es tal que 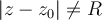 , entonces la serie de potencias es convergente si y solo sí es convergente absolutamente, y esto ocurre si y solo si
, entonces la serie de potencias es convergente si y solo sí es convergente absolutamente, y esto ocurre si y solo si 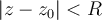 . En otras palabras, para series de potencias, cuando
. En otras palabras, para series de potencias, cuando 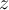 cae en el interior del disco de convergencia, la convergencia es absoluta. Cuando
cae en el interior del disco de convergencia, la convergencia es absoluta. Cuando 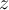 cae en el exterior no hay convergencia absoluta y tampoco convergencia (no absoluta) y cuando
cae en el exterior no hay convergencia absoluta y tampoco convergencia (no absoluta) y cuando 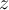 cae justo en el borde del disco de convergencia, puede pasar cualquier cosa.
cae justo en el borde del disco de convergencia, puede pasar cualquier cosa.