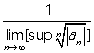en el archivo adjunto es la de los apuntes del Eleonora, hay alguna otra forma para calcularlo aparte de la formula adjunta?
Sí, hay otras formas de calcularlo. Hay otra fórmula parecida a esa de la raíz enésima, que proviente del criterio de D'Alambert para convergencia de series. No la escribo porque ahora no la recuerdo bien. Además siempre está el método de construir una serie de potencias usando la suma de la serie geométrica
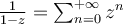
que demostramos en clase que converge si |z| < 1 y no converge si |z| >1. Entonces el radio de convergencia de la serie geométrica es 1 (por definición de radio de convergencia). Si uno tiene una serie de potencias que "proviene" de la geométrica, mediante algún cambio de variable, y/0 mediante integración término a término, y/o mediante derivación término a término, u otras operaciones, o una secuencia finita de esas operaciones, en cada una de ellas, uno va escribiendo al lado la bola abierta más grande donde converge, a partir de la de la serie geométrica. Y así, uno deduce el radio de convergencia final. Por ejemplo, tomemos el complejo a constante, y hallemos la serie de potencias centrada en 0, y su radio de convergencia, para la función:
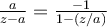
Haciendo el cambio de variables w = z/a, uno la lleva a la serie geométrica en w, que converge en la mayor bola abierta posible|w| < 1 . Luego que uno tiene esta serie, deshace el cambio de variables, para que quede todo en función de z, en vez de quedar en función de w, y tiene el desarrollo que converge en la mayor bola abierta posible |z| < |a|. Entonces el radio de convergencia de la serie de potencias de z, que se obtiene de desarrollar la función a/(z-a), será R= |a|.
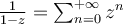
que demostramos en clase que converge si |z| < 1 y no converge si |z| >1. Entonces el radio de convergencia de la serie geométrica es 1 (por definición de radio de convergencia). Si uno tiene una serie de potencias que "proviene" de la geométrica, mediante algún cambio de variable, y/0 mediante integración término a término, y/o mediante derivación término a término, u otras operaciones, o una secuencia finita de esas operaciones, en cada una de ellas, uno va escribiendo al lado la bola abierta más grande donde converge, a partir de la de la serie geométrica. Y así, uno deduce el radio de convergencia final. Por ejemplo, tomemos el complejo a constante, y hallemos la serie de potencias centrada en 0, y su radio de convergencia, para la función:
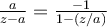
Haciendo el cambio de variables w = z/a, uno la lleva a la serie geométrica en w, que converge en la mayor bola abierta posible|w| < 1 . Luego que uno tiene esta serie, deshace el cambio de variables, para que quede todo en función de z, en vez de quedar en función de w, y tiene el desarrollo que converge en la mayor bola abierta posible |z| < |a|. Entonces el radio de convergencia de la serie de potencias de z, que se obtiene de desarrollar la función a/(z-a), será R= |a|.
(Editado por Eduardo Canale - sábado, 30 de abril de 2011, 21:31)
Para completar lo que escribí antes, si tengo una serie de potencias con radio de convergencia R, y la derivo, o la integro término a término, o la multiplico por una constante, o le resto sus primeros términos (una cantidad finita) entonces el radio de convergencia de la serie que se obtiene es el mismo.
Si tengo dos o tres o más series de potencias de (z-z_0) (todas series de potencias centradas en el mismo punto z_0), con coeficientes cada una los suyos,
y con radio de convergencia cada serie el suyo, entonces la serie de potencias que se obtiene sumando las que a mi me dieron, tiene como coeficiente enésimo, la suma de los coeficientes enésimos de las series que sumé, y tiene como radio de convergencia el mínimo de los radios de convergencia de las series que sumé.
Esas reglas a veces (no siempre, depende del ejemplo y del propósito que uno tenga, por ejemplo, si no son dados los coeficientes del desarrollo en serie de potencias de una función dada), esas reglas que expuse en este post y en el anterior, a veces, son más prácticas, que calcular el radio de convergencia con la fórmula de la raíz, u otras fórmulas.
Si tengo dos o tres o más series de potencias de (z-z_0) (todas series de potencias centradas en el mismo punto z_0), con coeficientes cada una los suyos,
y con radio de convergencia cada serie el suyo, entonces la serie de potencias que se obtiene sumando las que a mi me dieron, tiene como coeficiente enésimo, la suma de los coeficientes enésimos de las series que sumé, y tiene como radio de convergencia el mínimo de los radios de convergencia de las series que sumé.
Esas reglas a veces (no siempre, depende del ejemplo y del propósito que uno tenga, por ejemplo, si no son dados los coeficientes del desarrollo en serie de potencias de una función dada), esas reglas que expuse en este post y en el anterior, a veces, son más prácticas, que calcular el radio de convergencia con la fórmula de la raíz, u otras fórmulas.
Muchas gracias gracias por la respuesta
Se puede usar esta fórmula? De dónde sale? Gracias.
lim |a_n|/|a_n+1|
n -> infinito
a_n son los coeficientes de la serie.
lim |a_n|/|a_n+1|
n -> infinito
a_n son los coeficientes de la serie.
Sí, se puede usar perfectamente, cuando existe el límite ese.
Esa fórmula se demuestra a partir del criterio de D'Alambert de convergencia
de series numéricas de términos positivos.
Escribo aquí abajo el enunciado y la demostración de la fórmula que escribió Alejandro para calcular el radio de convergencia:
Hipótesis (H): Se tiene una serie de potencias
![\sum_{n= n_1} ^{+ \infty} a_n (z-z_0)^n \ \ \ \ \ \ \ \](https://eva.fing.edu.uy/filter/tex/pix.php/1a53a0beafc7d94e879a26074f233e0d.png "\sum_{n= n_1} ^{+ \infty} a_n (z-z_0)^n \ \ \ \ \ \ \ \")
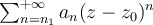.------------ . (A)
tal que existe (real finito o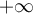
) el límite siguiente:
![R= \lim _{n \rightarrow + \infty} \frac{|a_n|}{|a_{n+1}|}\ \ \ \ \ \ \ \](https://eva.fing.edu.uy/filter/tex/pix.php/1ba9feff8cf823b5ed9491b78ef36ed8.png "R= \lim _{n \rightarrow + \infty} \frac{|a_n|}{|a_{n+1}|}\ \ \ \ \ \ \ \")
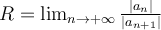.------------- . (R)
Tesis (T):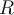
es el radio de convergencia de la serie de potencias (A).
Demostración:
Del curso de Cálculo 1, sabemos el criterio de D'Alambert, que dice esto:
Si
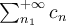. ---------. (B)
es una serie cuyos términos son números reales no negativos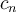
, y si existe (real o 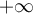} el límite
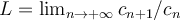
entonces:
-- Si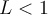
entonces la serie (B) converge.
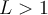-- Si
o si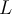 
es 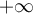entonces la serie (B) diverge.
-- Si
este criterio de D'Alambert no afirma nada sobre la convergencia de la serie (B).
Bueno, ahora tomemos la serie (A), y definamos la serie auxiliar (B) usando
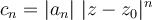. -------------------. (C)
(Observar que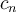 es real no negativo).
Usando la hipótesis (H) de que existe (real o +\infty) el límite (R), observamos
que
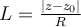. ------------------------(D)
¿Se entiende esta igualdad (D)?. Sale de la definición de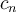 en la igualdad (C), para construir la serie auxiliar (B) como está dicho en el párrafo anterior, y de juntar el cálculo del límite según la igualdad (L), con la hipótesis (H) de que existe el límite según la igualdad (R).
Luego, aplicando el criterio de D'Alambert a la serie auxiliar (B) (que construimos a partir de la serie de potencias (A) dada en la hipótesis)
deducirmos que
-- la serie auxiliar (B) converge si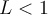, o sea si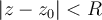 
--la serie auxiliar (B) diverge si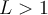, o sea si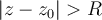 
Ahora, observamos que la serie auxiliar (B) es la serie de módulos de la serie de potencias (A). Entonces, si converge la serie auxilar (B), por definición de convergencia absoluta, la serie de potencias (A) converge absolutamente. (esto es converge la serie de sus módulos).
El teorema que dice que la convergencia absoluta implica la convergencia , con su demostración, igualita, vale para series de términos complejos en vez de restringirse a términos reales. Solo hay que sustituir, en ese enunciado y su prueba, módulo donde decía valor absoluto.
Entonces deducimos que
-- la serie de potencias (A) converge si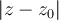
.------------- . ( I )
-- la serie de potencias (A) no presenta convergencia absoluta si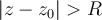![|z-z_0|>R\ \ \ \ \ \ \ \](https://eva.fing.edu.uy/filter/tex/pix.php/a8127af8d9c475baedfd8a8cc175b103.png "|z-z_0|>R\ \ \ \ \ \ \ \")
.------------- . ( II )
Finalmente recordamos que el teorema de existencia de radio de convergencia de una serie de potencias cualesquiera, dice que o bien la serie converge para todo
, en cuyo caso se dice que el radio de convergencia es 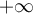, o bien, existe un único número real 
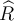tal que:
-- la serie de potencias converge y converge absolutamente para todo z tal que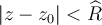
-- la serie de potencias no converge y no converge absolutamente para todo z tal que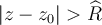
Por la unicidad del radio de convergencia, las afirmaciones ( I ) y ( II ) implican que el radio de convergencia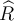 de la serie de potencias (A) debe ser igual al número 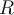que aparece en las afirmaciones ( I ) y ( II ). Este número 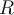era el definido en la igualdad (R). Se terminó de probar entonces que el radio de convergencia de la serie (A) se puede calcular con la fórmula dada en la igualdad (R). LQQD.
Como agregado que me parece que hay que recordar, enuncio las tres siguientes "recetas", sobre la teoría de series. (Las dos primeras se demuestran en forma similar a lo visto en series de Cálculo 1, pero usando complejos y sus módulos en vez de reales y sus valores absolutos. La tercera se demuestra igual que a lo que no sé si vieron en el curso de Ecuaciones Diferenciales sobre series de potencias de funciones de variable real):
--una serie de términos complejos cualquiera converge si converge absolutamente (o sea si converge la serie de los módulos, que es una serie de reales no negativos)
--existen series de términos complejos que convergen pero que no convergen absolutamente
--si una serie de términos complejos es una serie de potencias centrada en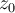
, que tiene radio de convergencia 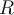, y si el valor de la variable z es tal que 
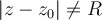, entonces la serie de potencias es convergente si y solo sí es convergente absolutamente, y esto ocurre si y solo si 
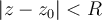. En otras palabras, para series de potencias, cuando cae en el interior del disco de convergencia, la convergencia es absoluta. Cuando cae en el exterior no hay convergencia absoluta y tampoco convergencia (no absoluta) y cuando cae justo en el borde del disco de convergencia, puede pasar cualquier cosa.
Esa fórmula se demuestra a partir del criterio de D'Alambert de convergencia
de series numéricas de términos positivos.
Escribo aquí abajo el enunciado y la demostración de la fórmula que escribió Alejandro para calcular el radio de convergencia:
Hipótesis (H): Se tiene una serie de potencias
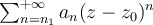.------------ . (A)tal que existe (real finito o
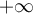) el límite siguiente: 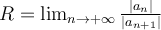.------------- . (R)Tesis (T):
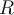es el radio de convergencia de la serie de potencias (A).Demostración:
Del curso de Cálculo 1, sabemos el criterio de D'Alambert, que dice esto:
Si
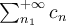. ---------. (B)es una serie cuyos términos son números reales no negativos
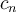, y si existe (real o 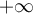} el límite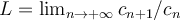 entonces:
-- Si
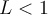entonces la serie (B) converge.-- Si
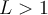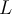o si es 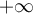entonces la serie (B) diverge.-- Si
este criterio de D'Alambert no afirma nada sobre la convergencia de la serie (B).Bueno, ahora tomemos la serie (A), y definamos la serie auxiliar (B) usando
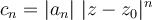. -------------------. (C)(Observar que
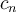es real no negativo).Usando la hipótesis (H) de que existe (real o +\infty) el límite (R), observamos
que
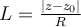. ------------------------(D) ¿Se entiende esta igualdad (D)?. Sale de la definición de
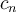en la igualdad (C), para construir la serie auxiliar (B) como está dicho en el párrafo anterior, y de juntar el cálculo del límite según la igualdad (L), con la hipótesis (H) de que existe el límite según la igualdad (R). Luego, aplicando el criterio de D'Alambert a la serie auxiliar (B) (que construimos a partir de la serie de potencias (A) dada en la hipótesis)
deducirmos que
-- la serie auxiliar (B) converge si
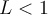, o sea si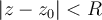 --la serie auxiliar (B) diverge si
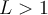, o sea si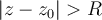 Ahora, observamos que la serie auxiliar (B) es la serie de módulos de la serie de potencias (A). Entonces, si converge la serie auxilar (B), por definición de convergencia absoluta, la serie de potencias (A) converge absolutamente. (esto es converge la serie de sus módulos).
El teorema que dice que la convergencia absoluta implica la convergencia , con su demostración, igualita, vale para series de términos complejos en vez de restringirse a términos reales. Solo hay que sustituir, en ese enunciado y su prueba, módulo donde decía valor absoluto.
Entonces deducimos que
-- la serie de potencias (A) converge si
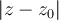.------------- . ( I )-- la serie de potencias (A) no presenta convergencia absoluta si
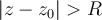.------------- . ( II )Finalmente recordamos que el teorema de existencia de radio de convergencia de una serie de potencias cualesquiera, dice que o bien la serie converge para todo
, en cuyo caso se dice que el radio de convergencia es 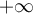, o bien, existe un único número real 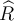tal que:-- la serie de potencias converge y converge absolutamente para todo z tal que
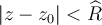
-- la serie de potencias no converge y no converge absolutamente para todo z tal que
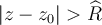
Por la unicidad del radio de convergencia, las afirmaciones ( I ) y ( II ) implican que el radio de convergencia
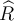de la serie de potencias (A) debe ser igual al número 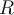que aparece en las afirmaciones ( I ) y ( II ). Este número 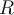era el definido en la igualdad (R). Se terminó de probar entonces que el radio de convergencia de la serie (A) se puede calcular con la fórmula dada en la igualdad (R). LQQD.Como agregado que me parece que hay que recordar, enuncio las tres siguientes "recetas", sobre la teoría de series. (Las dos primeras se demuestran en forma similar a lo visto en series de Cálculo 1, pero usando complejos y sus módulos en vez de reales y sus valores absolutos. La tercera se demuestra igual que a lo que no sé si vieron en el curso de Ecuaciones Diferenciales sobre series de potencias de funciones de variable real):
--una serie de términos complejos cualquiera converge si converge absolutamente (o sea si converge la serie de los módulos, que es una serie de reales no negativos)
--existen series de términos complejos que convergen pero que no convergen absolutamente
--si una serie de términos complejos es una serie de potencias centrada en
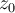, que tiene radio de convergencia 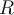, y si el valor de la variable z es tal que 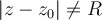, entonces la serie de potencias es convergente si y solo sí es convergente absolutamente, y esto ocurre si y solo si 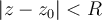. En otras palabras, para series de potencias, cuando cae en el interior del disco de convergencia, la convergencia es absoluta. Cuando cae en el exterior no hay convergencia absoluta y tampoco convergencia (no absoluta) y cuando cae justo en el borde del disco de convergencia, puede pasar cualquier cosa.