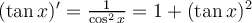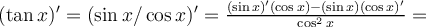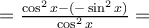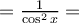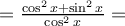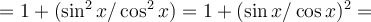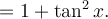En la tabla I del práctico 9 hay un error horrible, por favor corríjanlo:
La derivada de la función tangente de x es
En la tabla I del repartido 9, por error, aparece un 1 dividido algo en el último término de esa igualdad, por favor saquen el 1 dividido algo y dejen solo el algo, que es igual 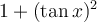 , sin ninguna división.
, sin ninguna división.
Veamos por qué es cierta esta igualdad, sabiendo que tan x es el cociente del seno dividido el coseno, usando la regla de derivada de un cociente, y sabiendo que la derivada del seno es coseno, y la derivada del coseno es menos el seno:
Gracias, disculpen por el error.