como hicieron la parte b? la verdad que ni idea llegue hasta lo que decia la sugerencia que te queda la tension hallada en a relacionado con la aceleracion de binet, pero despues de ahi ni idea
En respuesta a Sarah Jun Morioka Machado
Re: practico 4 ejercicio3
Vas bien encaminada.
Tenemos que
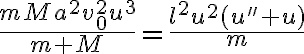
Igualando la fórmula de aceleración de Binet por la masa con la fuerza del hilo.
Usando que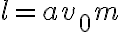 y acomodando un poco se llega a que
y acomodando un poco se llega a que
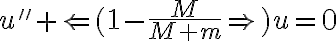
Esto da una solución cosenoidal con período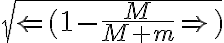 y fase 0 por las condiciones iniciales. Teniendo en cuenta que r es 1/u, para que llegue a pi, el coseno no se debe anular, ya que esto haría el radio irse a infinito, entonces de plantear
y fase 0 por las condiciones iniciales. Teniendo en cuenta que r es 1/u, para que llegue a pi, el coseno no se debe anular, ya que esto haría el radio irse a infinito, entonces de plantear
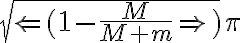 sale la condición
sale la condición 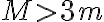
Tenemos que
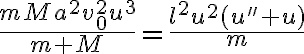
Igualando la fórmula de aceleración de Binet por la masa con la fuerza del hilo.
Usando que
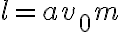 y acomodando un poco se llega a que
y acomodando un poco se llega a que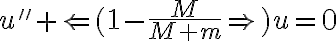
Esto da una solución cosenoidal con período
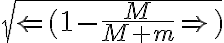 y fase 0 por las condiciones iniciales. Teniendo en cuenta que r es 1/u, para que llegue a pi, el coseno no se debe anular, ya que esto haría el radio irse a infinito, entonces de plantear
y fase 0 por las condiciones iniciales. Teniendo en cuenta que r es 1/u, para que llegue a pi, el coseno no se debe anular, ya que esto haría el radio irse a infinito, entonces de plantear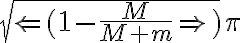 sale la condición
sale la condición 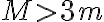
En respuesta a Yuri Damian Vallejo Iglesias
Re: practico 4 ejercicio3
muchisimas gracias!!
saludos
