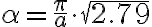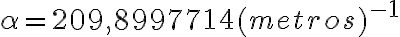Buenas, estaba haciendo este ejercicio y en la parte (b) me tranqué. Me da la impresión de que el ejercicio te pide que halles  usando
usando 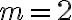 ,
, 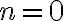 y que la frecuencia de trabajo es
y que la frecuencia de trabajo es 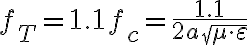
Bajo estas condiciones planteo 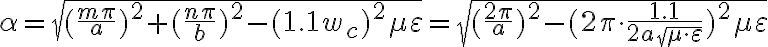
y llego a que  está exactamente dado por:
está exactamente dado por:
Lo cual numéricamente me da aproximadamente:
No encuentro forma de llegar al resultado de la solución a partir de esto. ¿Tiene sentido lo que estoy haciendo?
Saludos,
Alejandro