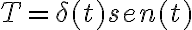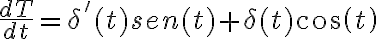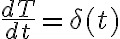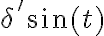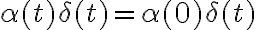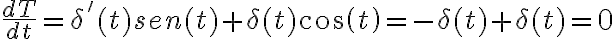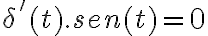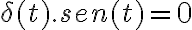sislin1: Practico 3 ejercicio 3.c

Estimados:

En la clase de hoy surgió una duda y me gustaría compartir a modo de desafío.

El problema es el siguiente,

quiero derivar la siguiente distribución:

1) Mediante la regla de la derivada del producto obtengo:

$\frac{dT}{dt}=\delta'(t)sen(t) +\delta(t)cos(t)$

2) Utilizando la propiedad de que 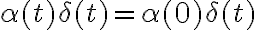$\alpha(t)\delta(t)=\alpha(0)\delta(t)$ y que el seno se anula en t=0 y el coseno vale 1 obtenemos el resultado:

$\frac{dT}{dt}=\delta(t)$

Cual es el error?

Saludos

Nacho

PD: El ejercicio 2 del práctico da una pista

Re: Practico 3 ejercicio 3.c

de Yamil Abraham Fernandez - viernes, 28 de marzo de 2014, 14:43

Hola! Soy el que planteó la duda hoy en clase. El problema es que la distribucion T es la distrib
ucion nula no?

Re: Practico 3 ejercicio 3.c

de Federico Mario Silva Abramo - viernes, 28 de marzo de 2014, 16:29

Hola,

T es la distribución nula, pero igualmente podés hacer cálculos y deberías llegar a que la derivada es nula también. Lo que yo hice fue plantear $\delta ' \sin(t)$ y hacer la derivada según la definición:

$=-$

$=- -$

Ahora sí podemos aplicar la fórmula $\alpha(t)\delta(t)=\alpha(0)\delta(t)$ en el último término y ver que se anula:

Entonces $\delta'(t) \sin(t)=-\delta(t) \cos(t)=-\delta(t)$

Por lo tanto, la suma de la derivada hecha con la regla del producto resulta

$\frac{dT}{dt}=\delta'(t)sen(t) +\delta(t)cos(t) = -\delta(t) + \delta(t)=0$

Creo que es por eso

Re: Practico 3 ejercicio 3.c

de Ignacio Irigaray - martes, 1 de abril de 2014, 00:05

Es basicamente eso. El error estaba en considerar que $\delta'(t).sen(t)=0$ , tal vez tentado por la similitud con $\delta(t).sen(t)=0$ igualdad que si se cumple. Es a lo que le dicen pensar rápido y mal!!!

Saludos