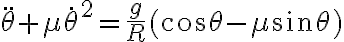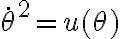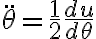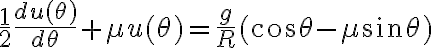Alguno me puede dar una mano con ese ejercicio? Tengo la ecuacion del movimiento, pero no se como usar la sugerencia (dθ/dt)2= u(θ) para hallar la velocidad en funcion de θ.
Gracias
Mirá a mi la ecuación de movimiento me quedó:
Ahí tenés que usar el cambio de variable 
. Si derivás ambos lados con respecto al tiempo y usás la regla de la cadena, llegás a que 
.
Entonces si sustituís en la ec. de movimiento te queda:
. Si derivás ambos lados con respecto al tiempo y usás la regla de la cadena, llegás a que .Entonces si sustituís en la ec. de movimiento te queda:
que es una ecuación lineal de primer orden no homogénea de la función u (que tiene variable 
)
)
Gracias Bernardo!!