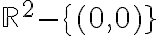Examen diciembre 2013 ej.1

Examen diciembre 2013 ej.1

de Gonzalo Alvaro Arcos Silva -
Número de respuestas: 4

Hola,

bueno nunca curse esta materia por lo que estoy estudiando de apuntes prestados para darla libre optativa, asique pido disculpas si lo que pregunto es un disparate.

No entiendo porque la integral del campo X tanto respecto a la curva C como respecto a la curva gamma es distinta de 0.

 Por el teorema de green no quedaria que  la integral del campo X respecto a una curva (sea C o gamma) es igual a la integral del rotor de X respecto al area S de la respectiva curva?

Entonces como X es irrotacional me queda la integral de 0 respecto del area S y eso me da 0.  Si alguien me pudiera decir que esta mal del razonamiento le agradezco!

 

Saludos

 

 

En respuesta a Gonzalo Alvaro Arcos Silva

Re: Examen diciembre 2013 ej.1

de Bruno Yemini -

Hola,

el problema es que el dominio del campo (\mathbb{R}^2 - \{(0,0)}) tiene un agujero y por lo tanto el teorema de Green no vale en ese dominio. En el práctico 4 se analiza un poco esta situación. Cualquier cosa, preguntá.
En respuesta a Gonzalo Alvaro Arcos Silva

Re: Examen diciembre 2013 ej.1

de Fernando Andres Figliolo Mederos -

mirá gonza, como el campo es irrotacional, la circulación a traves de una curva q encierre a (0,0) solo depende de la orientación de la curva y de cuantas vueltas efectue,

acá ves la curva:

http://www.wolframalpha.com/input/?i=Parametricplot3D%5B%7B%281%2B2t-t%5E2%29cos%282*pi*t%29%2C+%281%2B2t-t%5E2%29sin%282*pi*t%29%2C+0%7D%2C%7Bt%2C0%2C2%7D%5D

abrazo

En respuesta a Fernando Andres Figliolo Mederos

Re: Examen diciembre 2013 ej.1

de Marcos Razzetti Gomez -

tengo una duda, si el campo es irrotacional y la curva es cerrada y contiene todos los puntos la circulacion da 0 por green o stokes cual sea el caso.. eso se entiende, pero ponele que le falta un punto , porque la circulacion vale lo mismo para cualqueir curva que rodee? lo entiendo si es de gradientes pero si es solo irrotacional no entiendo proque