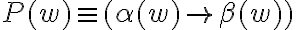"Y otra cosa ahí dice que que si # ocurre en w entonces P(aw) se cumple trivialmente, pero si en w hay una x despues del #?"
A mi tampoco me quedo muy clara su explicación, yo lo que pense fue que no es necsario mirar
el caso en que # pertenezca a w porque no se cumpliria la condicion del implica y por lo tanto eso haria verdadera la afirmación.
" Es necesario tomar el caso que pertenece `si la hipotesis dice que no?(o sea demostrar en todo el conjunto definido inductivamente y no solo en lo acotado, y en otros ejercicios habría que proceder así?"
No me quedo muy claro que fue lo que quisiste decir con eso, a que te referis con demostrar en todo el conjunto definido inductivamente y no solo en el acotado?
El PIP te dice que para demostrar una propiedad sobre todos los elementos de un conjunto y asegurarte que no te quede ninguno afuera tenes que demostrarla para los elementos que se forman aplicando las clausulas bases (PB) y luego a los que se forman aplicando las clausulas inductivas (PI). Por eso es que la propiedad se prueba para todo el conjunto.
Disculpa sino te respondi lo que preguntabas, cualquier cosa decime y vemos de vuelta :) saludos!